Evaluation AC2-01
Bluff body burner for CH4-HE turbulent combustion
Application Challenge 2-01 © copyright ERCOFTAC 2004
Evaluation
CFD results and Comparison against Experiments
The bluff-body burner here considered has been suggested and investigated experimentally by Masri, 1985. It is centred in a coflowing stream of air and consists of a circular bluff-body with an orifice at its centre for the main fuel Fig. 14. The diameters are 3.6 mm for the fuel nozzle and 50mm for the bluff-body. The main fuel jet composition is 50% CH4 and 50% H2 for a bulk Jet velocity of 118 m/s. The outer flowing air has a 40m/s velocity. The jet flame can be extinguished in a region downstream the recirculation zone where turbulence is well developed and the finite rate chemistry effects are significant. The flame may also reignite further downstream where turbulent mixing rates are relaxed. It should therefore be noted that, as observed by Masri, both the piloted and the bluff-body jet flames discussed here consist, generally, of three main zones: stabilization, extinction and reignition zones. The computation of this complex flow structure has been here addressed considering a more flexible unstructured grid. As for the pilot-jet flame, the axial symmetry of the problem is considered solving a single tangential sector of the cylindrical flow.
Figure 9:zoom of the unstructured mesh at inlet section
Figure 10: measured and computed recirculation streaklines
In this case, the elements on the plane section (Fig. 9) are triangles, which allow an easy clustering close to the bluff-body walls and especially at the sharp leading edges with the fuel and air jets. Being D the bluff-body external diameter, a total number of 11000 elements have been used for the discretization grid which has a 2.5xD radial dimension while the outlet plane is placed 5xD downstream the inlet section. The boundary conditions are specified with the same approach described in the previous test. The Flamelet database is obtained from the same reduced mechanism of the previous application.
Figure 11a:axial velocity Y/D=0.6 Figure 11b: axial velocity Y/D=0.9
Figure 11c: axial velocity Y/D=1.3
The steady convergence of the computation has not been obtained for the present case. In fact going on with the computation after the residual level of 10E-6 is firstly reached, then a cyclic behaviour of the convergence is observed. This effect has been associated to a pseudo-unsteady evolution of the flow field behind the bluff-body, which is apparently caused by the numerical discretization. The recirculation zone seems to be not numerically stable and periodically detaches from the bluff-body moving downstream towards the outlet section. Beside the downstream motion of this main recirculation vortex, a new one starts to develop at the bluff-body wall restarting the original flow pattern. It has to be pointed out that the present computation is not time-accurate. Moreover since no mention has been done of a similar phenomenon in the experiments results then this behaviour has to be considered a spurious numerical effect. Despite this fact, the minimum value of 10E-6 for the residual is reached when a single recirculation vortex is attached to the bluff-body wall as observed in the field from the experimental investigation. All the data shown in the following therefore refers to this condition.
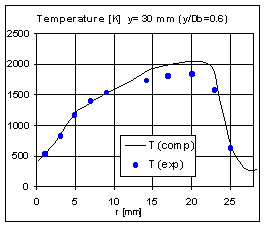
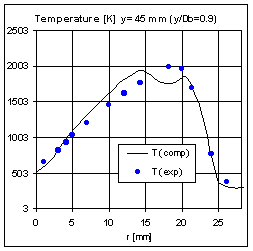
In Fig. 11, the velocity profiles are compared with experiments for three cross sections after the inlet. The accordance with measures is reasonably accurate showing that the main recirculation is correctly predicted by the numerical computation. This is qualitatively shown also comparing the flow pattern of Fig. 10. From computation it is also noticeable a small second vortex close to the fuel jet core as mentioned by Masri. The accurate simulation of the flow pattern reflects at the same instance a realistic representation of the turbulence field and therefore of the mixing properties behind the bluff-body which are to be expected in good agreement with experiments. As well known the conserved scalar approach is highly dependent on the turbulent mixing experienced by the reactants in the flow. The realistic simulation of this feature allows the correct prediction of the flame evolution and the accurate placement of the stoichiometric front. This can be observed in the following figures where the conserved scalar and temperature profiles are compared against experiments at several cross sections. Starting from the first section plane at Y/D=0.3 after the inlet, a peak is observed in the T profile inside the outer edge of the hot recirculation zone. This peak seems not present in the experiments and it is probably caused by the entrainment of unburned air flowing close to the bluff-body wall from the coflow stream directly into the main vortex core (Fig. 10).
Figure 12a: T profile Y/D=0.3 Figure 12b:scalar profile Y/D=0.3
Figure 13a: T profile Y/D=0.6 Figure 13b:scalar profile Y/D=0.6
Figure 14a: T profile Y/D=0.9Figure 14b:scalar profile Y/D=0.9
Figure 15a: T profile Y/D=1.3Figure 15b:scalar profile Y/D=1.3
Figure 16a: T profile Y/D=1.8Figure 16b:scalar profile Y/D=1.8
Figure 17a: T profile Y/D=2.4Figure 17b:scalar profile Y/D=2.4
Figure 18a: T axial r/D=0.12 Figure 18b: T axial r/D=0.8
This effect slightly reduces the mixture fraction concentration observed inside the vortex and for r»18 the presence of more air enhance the combustion producing the peak observed in the temperature. At the same instance the vortex outer branch seems to be more stretched by the entrainment of more fresh air in the core and again an overshoot of scalar mixture fraction, this time due to the excess of fuel, is observed from r»20 to r»24. Considering downstream sections the agreement with experiments is generally satisfying although a noticeable lower value of temperature is seen on the flame centreline for Y/D=1.3. Here a higher velocity of the fuel jet (observed from Fig. 11c) still maintains an efficient convective transport for the scalar field, which attains on the centreline a richer fuel-air ratio. This lag in the fuel jet spreading is probably due to the turbulence model response and it is soon recovered by the computation on the following sections as shown from the improved agreement of Fig. 14 and 18. A similar effect was above reported for the pilot-jet flame computation and seems to arise also for the present test concerning the turbulent field behaviour. In fact, although here less pronounced, the computation soon recovers from the under prediction of the scalar diffusion with a strong turbulent production which finally leads to a downstream excess of diffusion. This overdiffusion is clearly shown in Fig. 18 from the axial profile of the flame downstream about Y/D=120. In this case, the increased diffusion slightly reduces the level of the scalar mixture fraction crossing the flame front. Conversely, since quite lower turbulence production is expected within the fuel jet core then an accurate agreement is observed in Fig. 18 close to the flame centreline. This turbulence lag followed by a steep overproduction, although not pronounced as for the previous test, seems to be an intrinsic characteristic of the adopted turbulence model which becomes more critical when the grid is not enough refined and accurate as in the pilot-jet computation and as it starts to be for the section of Fig. 15. It has to be reminded that the large density fluctuations due to the combustion are here accounted in the flow computation simply through the density weighted averaging and no modifications were included into the original turbulent model suggested by Wilcox for inert conditions. Also the application of the eddy-viscosity approach becomes incapable of reproducing some important aspects of the physical flow such as the variable density-mean pressure gradients influence. Despite this evidence, the temperature and scalar profiles resulting from the present computation generally compare accurately with experiments.
Figure 19: radial distribution for species mass fraction, Y/D=0.3
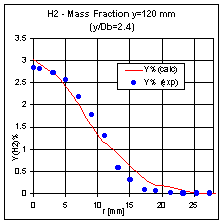
The average levels of main species are reported in Fig. 19, 20 and 21. A good agreement is shown for the O2 and H2 mass fractions in all sections considered. Conversely, a well-pronounced underproduction of CO and CO2 levels is characterising all the numerical prevision. The profiles are reproduced but the mass fraction levels are well below the experiments. This result for CO is to some extend surprising as it is known (Jones, 1994) that the fast chemistry assumption generally overestimates CO emissions especially on the rich side of the flame front.
This chemical mechanism is considered enough accurate for computing CO levels and therefore the source of the inaccuracy observed is more realistically though to be lying in the non-equilibrium effects associated with CO oxidation. In fact, CO is particularly dependent on the local stretch applied by the turbulent field on the laminar flame front.
Figure 20: radial distribution for species mass fraction, Y/D=0.9
Since an accurate prevision has been obtained for both the mixture fraction and the temperature of the flame then this effect has to be attributed to the chemical mechanism and to the Flamelet database computation. As far as the chemical reaction a 22-steps mechanism of CH4 involving 20 species has been considered.
Figure 21: radial distribution for species mass fraction, Y/D=2.4
The turbulent-chemistry interaction is only approximately accounted in the present model through a constant flame stretch for the whole field. This parameter is enforced during the counterflowing Flamelet computation imposing the relative reactants velocity. An increasing value for the flame stretch reduces considerably the amount of equilibrium species found at high temperatures. This explains why for CO the under prediction appears more relevant in the first sections and generally where higher temperatures are found in the hot burning gases. Having no priori information about the level of stretching to be expected in the flow field then it has been guessed using clearly a too high value. Although this effect has a little impact on the temperature profiles, it has a strong influence for CO and CO2 prediction.
Finally, in Fig. 22 the computed fields of temperature, mixture fraction and turbulent kinetic energy are reported showing the overall flame structure.
Figure 22: computed contours of T,![]() and k
and k
The numerical CFD solver HybFlow has been briefly described for simulation of internal turbulent reacting flows. Three application of the numerical procedure have been here described for turbulent non-premixed flames. General agreement with experimental data has been obtained for the turbulent CH4 bluff body flame experimentally studied at SANDIA although some discrepancies where observed in the temperature profiles. Apparently, the reason for these inaccuracies seems to be due to the strong response of the k-w turbulence model in the burning shear layer surrounding the fuel main jet. The low mach preconditioning approach of the solver performed efficiently for this particular flow condition where inlet velocity profiles have a fairly different magnitude that are ranging from about 40 m/s in the jet down to less than 1 m/s in the coflow air.
An accurate comparison against experiments has been performed for the bluff-body burner of Masri, 1985. In this test, the unstructured grid allowed a flexible disposition of the elements especially close the inlet streams and in the main recirculating vortex entraining the hot burning gases. This unstructured mesh features proved to be successfully allowing an accurate computation of the flow pattern developing behind the bluff-body as also of the mixture fraction and temperature profiles. Concerning the species mass fraction the miss prediction observed for CO and CO2 were attributed to an incorrect overestimation of the turbulent flame stretch within the Flamelet database assembly. In this regard, equilibrium phenomena resulted of considerable importance for the computation of CO emissions.
Further developments are still needed for a deeper analysis and understanding of the turbulence model performances for reacting flows. More computation will be then performed extending the application of the unstructured meshes which are promising greater flexibility and efficiency for the analysis of effective internal gas combustor geometries.