CFD Simulations AC4-01
Wind environment around an airport terminal building
Application Challenge 4-01 © copyright ERCOFTAC 2004
Overview of CFD Simulations
CFD calculations were carried out by NCSR Demokritos [CFD1] and University of Southampton [CFD2] to calculate the flow and turbulence in the wake of the terminal building at various points over the adjoining runway.
Simulations at NCSR Demokritos were performed by Panos Neofytou [Ref. 5], using ADREA_HF, a code developed and maintained in house, using a single equation, isotropic turbulence model. The boundary layer flow in the empty tunnel was modelled first, followed by a 3D simulation of the main terminal building, including other neighbouring buildings.
Simulations at the University of Southampton were carried out by James Forrest [Ref. 6], with the commercial code FLUENT using the standard k-ε turbulence model. Preliminary simulations of the boundary layer flow in the empty tunnel formed the basis for 2D and 3D calculations for main terminal building, using a simplified representation of its geometry and omitting surrounding buildings.
| NAME | GNDPs | PDPs (problem definition parameters) | SPs (simulated parameters) | |
|---|---|---|---|---|
| Re (full scale) | Wind direction | detailed data | DOAPs | |
| CFD 1 3D runaway wind environment simualtions (plus empty tunnel simulations) | 180, 150, 210 | Mean velocity, turbulence kinetic energy profiles | ||
| NAME | GNDPs | PDPs (problem definition parameters) | SPs (simulated parameters) | |
|---|---|---|---|---|
| Re (full scale) | Wind direction | detailed data | DOAPs | |
| CFD 2 2D and 3D runaway wind environments simulations (plus empty tunnel simulations) | ~5x106 | 180 | Ux, Uy, Uz, K | Mean velocity, turbulence kinetic energy profiles |
Table CFD-A Summary description of all test cases
References
[Ref. 5] P. Neofytou, A. G. Venetsanos, D. Vlachogiannis, J. G. Bartzis and A. Scaperdas "CFD Simulations of the Wind Environment around an Airport Terminal Building", Proc. of the Fourth International Conference on Urban Air Quality-Measurement Modelling and Management, Sokhi and Brechler (Eds), 2003.
[Ref. 6] Forrest J. (2003) CFD for the airflow around an airport terminal building, MEng project report, University of Southampton.
Simulation Case CFD1
Solution strategy
The ADREA_HF (version 1.2) code was employed to carry out the CFD calculations in neutral atmospheric stability conditions.
The solution strategy consisted in solving the transient, Reynolds averaged, mass and momentum 3D conservation equations for the mean flow, until steady state conditions were reached.
Turbulence was modelled using an isotropic one-equation model [Ref. CFD1-1]. Turbulent diffusivities were obtained using the Boussinesq assumption, with the turbulent kinetic energy obtained from its conservation equation. The length scales were calculated from algebraic relations, which in the general case depend on the distance from solid surfaces, the atmospheric stability and the asymptotic pressure gradient.
The set of conservation equation as applied to this particular case, solved by the ADREA-HF, is the following:
Total mass:
Failed to parse (syntax error): {\displaystyle \[\frac{\partial\rho}{\partial {t}} + \frac{\partial\rho U_{i}}{\partial {X}_{i}} = 0\]}
Momentum:
Failed to parse (syntax error): {\displaystyle \[\frac{\partial PU_{i}}{\partial} + \frac{\partial PU_{i} U_{j}}{\partial x_{j}} = -\frac{\partial {P}}{\partial x_{i}} + \frac{\partial}{\partial x_{j}}\left(pK_{m} \frac{\partial U_{i}}{\partial x_{j}}\right)\]}
The isotropic turbulence model used for this work is a single equation model:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbases.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \[K_{mx} = K_{my} = k_{mz} = K_{m}\]}
Where Kmi for i=x, y, z denote the turbulent diffusion coefficients. The eddy viscosity Km is calculated as follows:
Failed to parse (syntax error): {\displaystyle \[k_{m} = C_{m}\kappa^{1/2\imath}\]}
for Failed to parse (syntax error): {\displaystyle \kappa\succ 0\]}
k is the turbulent kinetic energy and l is the turbulence length scale.
In line with other investigators [Ref. CFD1-7], the empirical constant Cm=0.1887 is calculated from the near wall one-dimensional neutral flow, and the length scale l is set equal to the wall distance z. Using Kz=ku*z , the near wall turbulent kinetic energy approximation [Ref. CFD1-8]kw=4.495u*2 and the above equation Cm can be derived
The turbulent kinetic energy is calculated using the equation below:
Failed to parse (syntax error): {\displaystyle \[\frac{\partial p\kappa}{\partial} + \frac{\partial pu_{j}\kappa}{\partial x_{j}} = \frac{\partial}{\partial x_{j}}\left(p\frac{K_{m}}{\sigma_{x}} \frac{\partial k}{\partial x_{j}}\right) + G-pE\] }
sk=1, ε is the viscous dissipation rate, G represents the turbulence generation term as follows:
Failed to parse (syntax error): {\displaystyle \[G = -\overline{pu_{i}u_{j}} \frac{\partial u_{i}}{\partial x_{j}}\]}
Failed to parse (syntax error): {\displaystyle \[E = C_{D} \frac{\kappa^{3/2}}{\imath}\]} CD=0.242
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbases.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \[-\overline{pu_{i}\prime u\prime_{j}} = K_{m} {(\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})} -\frac{2}{3}\delta_{ij}\kappa\]}
Failed to parse (syntax error): {\displaystyle \[\frac{1}{\imath} = \Bigg(\bigg(\frac{1}{\imath_{g}}\bigg)^{n} + \bigg(\frac{1}{\imath_0}\bigg)^{n}\Bigg)^{1/n} ; {n} = 5\]}
Failed to parse (syntax error): {\displaystyle \[\imath_0 = C_{\Gamma}\frac{\kappa}{\Gamma}\]}
; CG =0.49
Failed to parse (syntax error): {\displaystyle \[\Gamma = \frac{1}{\rho}\bigg(\sum\limits_{i}\Big(\frac{\partial P}{\partial x_{i}}\Big)^2\bigg)^{1/2}\]}
lg is the minimum distance from the ground, G is the asymptotic pressure field acceleration parameter.
The discretisation method applied was the “control volume” approach [Ref. CFD1-9], whereby equations are integrated into control volumes. A staggered grid is used for the momentum equations. The fully implicit first order scheme is used for time discretisation. The first order upwind scheme was used for the convection terms. The coupled set of conservation equations was solved, by applying an iterative procedure at each time step.
Computational Domain
The computational domain used for the calculations is shown in the figure below.
Figure CFD1-1: The computational domain for CFD1 simulations
The mesh was constructed using the DELTA-B pre-processor [Ref. CFD1-5]. It encompasses all buildings close to the tested measurement locations and reproduces nearly all the detail in the CAD geometry supplied (as discussed earlier in EXP1) and is thus an accurate representation of the test geometry in the wind tunnel. It consists of a 850x850x200m area discretised as a 52x54x50 grid, which is refined near the measurement points and near the buildings.
The CFD model geometry is only slightly different to the actual wind tunnel geometry in that it was simplified very slightly to omit some small scale detail, and the terminal building has no openings to allow any through flow. It is unlikely that these simplifications should affect the DOAPs
Boundary Conditions
Boundary conditions for the 3D problem were zero gradient for the outflow boundaries, wall functions at the building surfaces and the ground, and zero vertical velocity at the top of domain.
A preliminary 1D calculation was carried out to obtain appropriate inlet profiles of dimensionless velocity and turbulence kinetic energy (TKE) for the 3D calculations. The results are shown in Figure CFD1-2. Velocities are non-dimensionalised with respect to the value at 10m of the undisturbed field, i.e. in an empty tunnel in the absence of buildings upstream. Turbulence kinetic energy is normalised by the square of the streamwise velocity at 10m in an empty tunnel.
The velocity profile obtained was in good agreement with the experiment, but the predicted normalised turbulence kinetic energy was significantly lower, the value at 10m being approximately 0.013 instead of 0.022 in the experiment. Assuming a logarithmic layer velocity profile with roughness 0.006m, one can obtain 4.5 and 7.6 for from the above values of . The value of 7.6 is considered large compared to 4.5 suggested by Monin and Yaglom [Ref. CFD1-3]and used in the present model [Ref. CFD1-2].
Figure CFD1-2: Comparison of the dimensionless profiles of the velocity (left) and TKE (right) for the undisturbed flow field.
Application of Physical Models
In line with other investigators, the concept of surface layer functions has been adopted in ADREA-HF to avoid an excessive number of cells near the ground, due to very steep parameter gradients, occurring at this region. Analytical functions of normal distances sn near the ground are used to describe the parameters under consideration. The relations adopted are mainly extrapolations of the one-dimensional surface layer relations [Ref. CFD1-10]. The friction velocity, u*, is given by the relation:
Failed to parse (syntax error): {\displaystyle \[u\diamondsuit = \frac{V_{t}{(s_{n})}}{\Psi_{m}{(s_{n})}}\]}
The velocity Vt is the velocity component parallel to the surface. Evaluation of this velocity is based on the surface orientation. Thus, Vt is the tangential velocity for flat.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbases.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \[\Psi_{m} = \int^{s_{n}}_{s_0}\frac{\Phi_{m}{(s)}}{s} {ds}\]}
where s0 is the surface roughness. For neutral flows Fm(s)=1, so
Failed to parse (syntax error): {\displaystyle \[\Psi_{m} {(s_{n})} = \frac{1}{\kappa} 1n \frac{s_{n}}{s_0}\]}
The expression for the turbulence kinetic energy, k, near the ground, has been obtained by assuming turbulent kinetic energy diffusion processes to be negligible compared to generation and dissipation processes, so that:
Failed to parse (syntax error): {\displaystyle \[\kappa {(s_{n})} = 4.495u^2_\ast\]}
Numerical Accuracy
Iteration convergence of the outer iterations (i.e. outermost loop within a time step), was based on maximum relative errors being less than 0.001 and total mass balance normalized by the total flow in being less than 0.05.
Iteration convergence of the inner iterations within a conservation equation was based on maximum relative errors being less than 10-6. No under-relaxation factors were used.
CFD Results
The mean velocity and turbulence kinetic energy profiles, with and without the buildings, are used to compare and evaluate the CFD results. These are presented in graphical format only, no datafiles are provided.
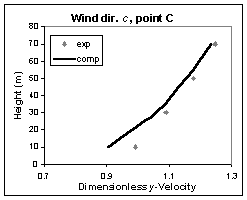
The results of the 3D calculation are presented in Figures CFD1-3 to Figures CFD1-5 below. The x- and y-components are normal and parallel to the runway respectively. Three wind directions were simulated, a (=210°), b (=180°, incidence normal to building), and c (=150°), and the CFD results presented in the figures correspond to measurement points A, B and C, at various heights over the runway. Velocities are non-dimensionalised with respect to the value at 10m of the undisturbed field, i.e. in an empty tunnel in the absence of buildings upstream. Turbulence kinetic energy is normalised by the square of the streamwise velocity at 10m in an empty tunnel.
Figure CFD1-3 shows the predicted normalised y-velocity profiles for wind directions a, b, and c compared with experiment. Figure CFD1-4 shows the corresponding profiles of normalised x-velocity for directions a and c. The model predicts a larger reduction of the velocity in the wake of the building for direction b, in agreement with the experiment. The figures also show that the model has the tendency to underestimate the effect of the buildings for the wind direction normal to the building (direction b), while better agreement with experiment is obtained for oblique incidence directions a and c.
Figure CFD1-5 presents the predicted profiles of turbulence kinetic energy for the three wind directions (WD) a to c. The predicted turbulent kinetic energy for direction b is higher than in the other cases and this is consistent with the turbulence measurements. It is also consistent with the higher velocity profile distortion observed experimentally for direction b. For all three wind directions however, the model overpredicts the turbulence by up to about a factor of two.
Figure CFD1-3: Comparison of y-velocity profiles.
Figure CFD1-4: Comparison of x-velocity profiles.
Figure CFD1-5: Calculated dimensionless TKE for wind directions a, b and c compared against experimental data.
References
[Ref. CFD1-1] Andronopoulos, S., Bartzis, J. G., Würtz, J. and Assimakopoulos, D., 1993
Simulation of the Thorney Island dense gas trial No. 8, using the code ADREA-HF, Process Safety Progress 12, 61-66.
[Ref. CFD1-2] Bartzis J. G., 1989 Turbulent diffusion modeling for wind flow and dispersion, Atmos. Environ. 23, 1963-1969.
[Ref. CFD1-3] Monin A. S., Yaglom A. M. (1973) Statistical Fluid Mechanics. The MIT Press, Cambridge, MA.
[Ref. CFD1-4] Venetsanos A.G., D. Vlachogiannis, A. Papadopoulos, S. Andronopoulos, J.G. Bartzis, 2002 Studies of pollutant dispersion from moving vehicles, Water, Air and Soil Pollution-Focus 2, 325- 337.
[Ref. CFD1-5] Venetsanos, A.G., Catsaros, N., Würtz, J. and Bartzis, J. G., 1995 The DELTA_B code. A computer code for the simulation of the geometry of three-dimensional buildings. Code structure and users manual, Report EUR 16326 EN.
[Ref. CFD1-6] Vlachogiannis D., Rafailidis S., Bartzis J.G., Andronopoulos S., Venetsanos A.G., 2002 Modelling of Flow and Pollution Dispersion in Different Urban Canyon Geometries, Water Air and Soil Pollution Focus 2, 405-417.
[Ref. CFD1-7] Launder B. E., Spalding D. B., (1972), “Mathematical models of turbulence”, Academic Press, New York.
[Ref. CFD1-8] Monin A. S., Yaglom A. M., (1973), “Statistical fluid mechanics”, Vol. 1, p. 210, the MIT press, Cambridge, MqA.
[Ref. CFD1-9] Patankar S.V., (1980), ‘Numerical Heat Transfer And Fluid Flow’, Hemisphere Publishing Corporation, Washington.
[Ref. CFD1-10]Pielke R.A., (1981), ‘Mesoscale numerical modelling’, Advances in Geophysics, Vol 23, pp 2144.
Simulation Case CFD2
Solution strategy
The commercially available CFD code FLUENT (version 5) was used [Ref. CFD2-1]. The incompressible, isothermal RANS equations were solved, using the standard k-ε turbulence model with standard constants, and standard wall functions The numerical discretisation scheme used was second-order. The default pressure-velocity coupling algorithm SIMPLE, and the ‘segregated’ solver option, were employed.
Computational Domain
Three meshes were constructed: an empty tunnel box in 2D to simulate the empty tunnel, and two models of the main terminal building, in 3D and 2D. The geometry of the terminal building was simplified to the 2D shape shown in Figure CFD2-1, and this profile was extruded to create the 3D shape. The terminal building was modeled in isolation; neighbouring buildings were not included to simplify the CFD mesh. This omission will affect the flow locally, and since the neighbouring buildings are situated upstream of the terminal building and their heights are relatively low compared to the main building (~0.3H), it anticipated that the overall shape and dimensions of the wake will be primarily influenced by the geometry of the terminal building rather than that of the neighbouring buildings. As a result, the DOAPs for this Application Challenge, i.e. the velocity defect and turbulence intensity at the runway will probably be unaffected.
Figure CFD2-1: Simplified 2D profile for the main terminal building
Empty tunnel 2D mesh: A regular hexahedral 2D mesh was created, to simulate the flow in the empty tunnel, as illustrated in Figure CFD2-2 The first vertical node was placed at z/δ=0.0229 and a further 34 nodes placed according to a logarithmic profile so that the spacing between the topmost node and the top of the domain was z/δ=0.086.
Figure CFD2-2: 2D empty tunnel mesh
3D mesh: Only half of the building was modeled, placing a symmetry boundary along the y-z plane at half the building length (as illustrated in Figure CFD2-3).
The computational domain around the building was a rectangular box which extended 20H upstream of the building, 50H downstream, and 10H above. This is much more extensive than the recommendation by Cowan et al. [Ref. CFD2-2] that the computational domain around a building should not be smaller than 5H upstream and 15H downstream, since the runway was positioned 14H downstream of the building and therefore had to be kept sufficiently away from the outlet. Increased refinement was used in a region 3H high and 7H long around the building, where a grid spacing of Δm=0.5m=1.4%H was used. This was chosen to fulfill the criterion of 1%H recommended by Castro et al. [Ref. CFD2-3] to fully resolve the shear layer in separated flows. Elsewhere in the domain a gradual expansion ratio (less than 1.2) was used. Additional embedded refinement was also used to refine the mesh around the leading edge of the roof and the raised section, as illustrated in Figure CFD2-5. A cross-streamwise width of 8H was used; Cowan et al. [Ref. CFD2-3] recommended that this should not be smaller than 4H. The mesh consisted of tetrahedral cells around the building, but further from the building a Cartesian grid was used, as illustrated in Figure CFD2-4. The total number of cells was ~2x106.
Figure CFD2-3: The extruded 3D building geometry (mirrored at the line of symmetry)
Figure CFD2-4: Detail of the mesh discretisation around the 3D building geometry
Figure CFD2-5: Local refinement around the leading edge of the roof and the raised section
2D mesh: In addition to the 3D mesh, a 2D mesh of similar domain size and mesh refinement was created, to illustrate the differences between a 2D and 3D solution. Tetrahedral cells were used throughout and the total number of cells was ~90,000.
Boundary Conditions
The zero gradient condition was specified at the outlet, and symmetry boundaries were specified at the top and sides of the domain. The position of the inlet and outlet boundaries was placed at a distance well away from the building and the measurement location, as discussed in the previous section. The wall surfaces were modeled using wall functions; the ground plane was modeled as a rough wall, the aerodynamic roughness matching that simulated in the wind tunnel, and using a smooth wall roughness for the building walls.
Much effort was invested in defining appropriate inlet conditions, i.e. appropriate vertical profiles of velocity, k and ε. Although it was possible to replicate the mean velocity profile measured in the wind tunnel, the CFD profiles for k underestimated the measured values.
The following two approaches were considered:
BL1: profiles of U, k and ε were taken from a distance of 25H downstream of the inflow boundary. These were used as inlet boundary conditions for another flow computation. A modified value of Cμ=0.0163 was used to match the wind tunnel value of k at the wall based on:
Other constants Cε1, and Cε2 were left unchanged. Once the solution had converged, profiles of U and k were examined at various locations, and were found to remain constant along the domain.
BL2: the established method of Castro and Apsley [Ref. CFD2-4] was used whereby:
z<0.9h
z>0.9h
and
Failed to parse (syntax error): {\displaystyle \[E = \frac{c_{\mu}^{3/4} \kappa^{3/2}}{\kappa Z}\]}
using the default value of Failed to parse (syntax error): {\displaystyle \[C_{\mu} = 0.09\]}
.
In FLUENT [Ref. CFD2-1] the roughness of the wall is specified via a wall roughness height, Ks, and a roughness constant, CKs, rather than the aerodynamic roughness z0, though these are roughly related via the expression:
Failed to parse (syntax error): {\displaystyle \[z_{0}\approx \frac{CKs Ks}{E}\]}
where E is an empirical constant set to 9.81. An appropriate range of values for CKs =0.5 to 1, and CKs=1 was chosen, and Ks was set to give a value of z0 which most closely matched the experimental data.
Profiles BL1 and BL2 are plotted in Figure CFD2-6, compared against experimental values. The velocity profile for BL2 matched the experimental one closely, but the k-profile values are much lower than the experimental ones. The velocity profile for BL1 departs slightly from the experimental one, and though the k values are larger than those obtained with BL1 and are correct at the wall, the profile is still significantly different to that measured. Possible reasons for the discrepancy could be a deficiency in the k-ε model, the need to modify constants other than Cμ. However, it is also possible that the boundary layer created in the wind tunnel was still developing and had not reached equilibrium, i.e. the wind tunnel boundary layer conditions were inappropriate for the purposes of this study.
Figure CFD2-6: Comparison of mean velocity profiles for simulated boundary layers BL1 and BL2.
Figure CFD2-7: Comparison of k profiles for simulated boundary layers BL1 and BL2.
Application of Physical Models
Standard wall functions were applied at wall surfaces, as described in ‘Boundary Condition’ above. Details of the mesh distribution near the walls and y+ values were not reported.
Numerical Accuracy
The convergence criterion used was reducing scaled residuals to below 10-5, and this was achieved for both the 2D and 3D simulations. This level of convergence (which is well below the default 10-3 value used in FLUENT) was deemed necessary to obtain results that were numerically accurate; during preliminary simulations of the boundary layer evolution in the empty tunnel geometry it was found that the boundary layer shape near the outlets was distorted when residuals were greater than 10-4.
CFD Results
The mean velocity and turbulence kinetic energy profiles, with and without the buildings, are used to compare and evaluate the CFD results. These are presented in graphical format only; no datafiles are provided.
3D simulations:
The comparison of U and k profiles at the runway location, normalised by the free-stream velocity U0,is shown in Figure CFD2-8. Note that this normalisation is different to that used to non-dimensionalise the experimental values (relative to ‘empty tunnel’ data).
The mean velocity profile agrees well with experimental data (within 5-10%). The k profile is in partial agreement with the data, and the k peak occurs at a lower value than the tunnel data. The simulated and experimental maximum values of k/Uo2 are similar, but this agreement is most probably coincidental and the result of the much lower levels of turbulence prescribed at the inlet balancing the over-generation of turbulence around the building. The numerical model predicts a 400% increase in k compared to the empty tunnel case, which is well above the 50-60% increase in the experimental data. Thus, the increase in turbulence (DOAP2) is over-predicted by a factor of 5.
The inadequacies of the k-ε turbulence model with regards to excessive k production are well-documented and could be the reason underlying the excessive turbulence production. In areas of high streamwise strain rates which occur around bluff bodies the k-ε model is known to fail to model the turbulence dissipation adequately and therefore over-predicts the turbulence kinetic energy in those areas. Figure CFD2-9 illustrates the areas in the solution where the turbulence energy is created, namely upstream of the leading edges of the roof and around the raised section.
Figure CFD2-8: Comparison of 3D simulation results (U/Uo and k/Uo2) with experimental data (See CFD2-8.jpg for an enlarged view of the figure above)
Figure CFD2-9: Turbulence energy isosurface for k/U0=0.33.
2D simulations: these were preliminary simulations preceding the 3D simulations. They were initially run using the BL1 inlet conditions but the solution gave physically unrealistic results and subsequently diverged. For this reason, the use of BL1 was abandoned and all subsequent simulations in 2D and 3D were carried out using BL2.
The comparison of U and k profiles at the runway location, normalised by the free-stream velocity U0,is shown in Figure CFD2-10. The mean velocity profiles simulated with and without the building are virtually identical, suggesting that the building had no effect on the mean velocity profile at the location of the runway. The comparison of the k profiles at the runway location shows that the simulation under-predicts the turbulence levels in the building wake. However, as with the 3D simulations, the 2D simulation overpredicts the increase in turbulence (DOAP2), by a factor of 2. Therefore, the reason for the lower overall turbulence levels is due to much lower levels of turbulence in the incident wind profile prescribed at the inlet (BL2) compared to the experimental profile.
Velocity profiles from the 2D solution were examined at locations between the building and the runway. Though a noticeable velocity deficit did occur in the wake of the building, the mean velocity had ‘recovered’ before reaching the runway, at about ~14H. This premature recovery is clearly contrary to results from other experimental studies. A study by Castro ([Ref. CFD2-5], see also UFR3-14) of the wake effects of a 3D bluff body immersed in a 2D boundary layer suggest that for a body of similar size, recovery of the mean velocity profile should be expected after a distance of ~50H downstream.
The point at which the flow reattaches on the ground downstream of the building was also estimated by inspection of the streamline diagrams (Figure CFD2-11). This was found to be equal to 3H, which is too short compared to Castro’s data for a bluff body submersed in a boundary layer. Again, the over-prediction of turbulence by the k-ε model is probably the cause of this premature re-attachment. As unphysically high levels of turbulence are transported downstream, they are thought to cause an increase in the mean velocity as momentum is transferred from high k areas to parts of the boundary layer that have been retarded by the building.
It is therefore clear that, in contrast to the 3D simulation, the 2D simulation predicts recovery of the mean velocity profile at a much shorter distance downstream of the building, thus failing to predict the velocity defect at the runway (DOAP1).
Figure CFD2-10: Comparison of 2D simulation results (U/Uo and k/Uo2) with experimental data (See CFD2-10.jpg for an enlarged view of the figure above)
Figure CFD2-11: 2D simulation – velocity vector diagram for 2D flow around the terminal building
References
[Ref. CFD2-1] FLUENT Users’ Guide July 1998, Fluent Inc.
[Ref. CFD2-2] Cowan I. R., Castro I. P., Apsley D. D. (1997) “Numerical considerations for simulations of flow and dispersion around buildings” Journal of Wind Engineering and Industrial aerodynamics, Vol. 67&68, pp. 535-545.
[Ref. CFD2-3] Castro I. P. Cowan I. R. and Robins A.G. (1999) “ Simulations of flow and dispersion around buildings” Journal of Aerospace Engineering, pp. 145-160.
[Ref. CFD2-4] Castro I. P. and Apsley D. D. (1997) Flow and dispersion over topography: a comparison between numerical and laboratory data for two dimensional flows” Atmospheric Environment, Vol. 31, No. 6, pp. 839-850
[Ref. CFD2-5] Castro I. P. (1979) “Relaxing wakes behind surface-mounted obstacles in rough wall boundary layers” Journal of Fluid Mechanics, Vol. 93, Part 4, pp.631-659.
© copyright ERCOFTAC 2004
Contributors: Athena Scaperdas; Steve Gilham - Atkins
Site Design and Implementation: Atkins and UniS