UFR 2-11 Description
High Reynolds Number Flow around Airfoil in Deep Stall
Flows Around Bodies
Underlying Flow Regime 2-11
Description
Introduction
The high Reynolds number flow around airfoils at large (beyond stall) angles of attack is a challenging CFD problem of significant importance for the aerospace industry. Nonetheless, up to the late 90s of the last century, the studies providing quantitative data on this type of flow were, first, exclusively experimental and, second, rather limited. The lack of CFD studies was caused by the inability of RANS turbulence models of any level of complexity to represent such massively separated flows, on one hand, and by an unaffordable computational cost of LES of such flows, on the other hand. The limited character of the early experimental studies is explained by the difficulties of measuring unsteady flow characteristics. For instance, the textbook of Hoerner [6] provides only the mean lift and drag coefficients. The same is to a considerable extent true for the later experiments of Sheldahl and Klimas (1981) [20] and of Raghunathan et al. (1988) [16] (see Table 1).
More systematic studies of the considered UFR, both computational and experimental, were started towards the end of the last century, when the growth of the computer power and emergence of appropriate modelling approaches (e.g., Detached-Eddy Simulation (DES) [24, 26] and Scale- Adaptive Simulation (SAS) [10, 11]) and measurement techniques capable of capturing unsteady flow features made this possible.
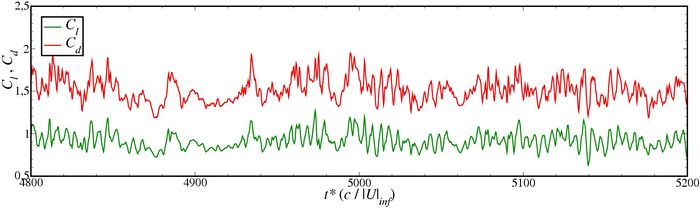
The key physics of this UFR is predominantly characterised by the unsteady, three-dimensional, massively-separated wake region. This takes the form of a nominally periodic shedding of large scale, coherent vortices in a vortex street pattern, which is overlaid with finer random turbulent fluctuations at higher frequencies and random modulation and intermittency at frequencies lower than the vortex shedding frequency. A visual impression of these features is given in Figure 1. It has been found that it is necessary to capture these key physical features in a simulation, not just for the prediction of unsteady quantities but even in order to reliably predict steady-state parameters such as the mean force coefficients.
| Figure 1: Figures to accompany the description of the key flow physics of the UFR. Snapshot of vorticity magnitude from a finely-resolved DES of the UFR [13] (above) and experimental time traces of lift and drag coefficient [27, 28] (below). |
The document starts from an overview of the past studies of the
considered UFR and a justification of the choice of the primary test
case (NACA0021 airfoil at 60° angle of attack, experiments of Swalwell et al.
[27, 28]).
A more detailed outline of the experiment is then
given, after which a summary of CFD methods used, major results of the
simulations and their comparison with the experimental data are
presented. Following this, in the BPA section, the effects of the
parameters of the simulations to which the results show the greatest
sensitivity are discussed and BPA are formulated. A twofold purpose of
the UFR and BPA are envisaged:
- Provision of information regarding the best class of turbulence modelling strategy, accompanying numerical framework and simulation setup for the practitioner simulating analogous flows.
- Thorough documentation of a test case suitable for the verification of either new developments or new implementations of turbulence-resolving approaches, e.g. in the hybrid RANS-LES family.
Due to the importance of the highly unsteady wake in this UFR, it is
considered of relevance to this aspect of the following Application
Challenges:
Review of UFR studies and choice of test case
The key physical characteristics of the UFR (Section 1) present significant challenges to conventional turbulence strategies: to (U)RANS in terms of solution fidelity and to full LES in terms of computational expense (assuming that the turbulent boundary layers are to be resolved). The flow is furthermore of significant relevance to many applications in (but not limited to) the aerospace industry. As such, when the now-prominent hybrid RANS-LES methodology known as Detached-Eddy Simulation (DES) was proposed [26], which sought to address these shortcomings of RANS and LES, the flow over an airfoil in deep stall was selected to test and demonstrate the improvements achieved [22]. Since then, the same or similar flows were employed in numerous collaborative research studies by partners proposing new turbulence-resolving methods or seeking to verify new implementations of existing methods.
The following bullet points provide a brief review of past CFD studies of this UFR (in chronological order of publication):
- First true application of DES (Shur et al., 1999 [22]): NACA0012 airfoil, Re = 1.0×105, angle of attack, α, ranging from 0° to 90°, spanwise domain Lz = 1 chord length (c).
- Significant improvement of DES over URANS shown. The findings were recently revisited in light of current knowledge and upheld [2].
- Analogous study with evidence of span size sensitivity (Guenot, 2004 [3]): case as above, but α = 45°, variation 0 ≤ Lz ≤ 4c.
- Use of the NACA0012 (α = 45°) test case to examine the role of numerics in DES (Shur et al., 2004 [23]).
- EU FLOMANIA project (Haase et al., 2006 [4]): as above but α = 60° and Lz = 1c.
- Large international validation exercise (11 partners).
- High robustness of DES to different CFD codes and underlying RANS models.
- EU DESider project (Haase et al., 2009 [5]): switch to NACA0021 at α = 60°, Re = 2.7×105, variation 0 ≤ Lz ≤ 4c.
- More thorough investigation of principal test case sensitivities (Garbaruk et al., 2010 [2]): results from NACA0021 test case, review of experiments including NACA0012.
- Span size and time sample identified as principal sources of uncertainty.
- Statistical error as function of time sample length quantified.
A review [2] of past experimental studies of the UFR is given in Table 1.
| Reference | Airfoil profile | Spec | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hörner [6] | 0012 | 1.0 | 180° | 0.92 | 1.65 | — | — | — | — |
| Raghunathan et al. [16] | 0021 | 2.6 | 90° | 0.82 | — | — | — | — | — |
| Sheldahl & Klimas [20] | 0012 | 3.6 | 180° | 0.875 | 1.470 | — | — | — | — |
| 0015 | 3.6 | 180° | 0.875 | 1.470 | — | — | — | — | |
| 0021 | 3.6 | 180° | 0.875 | 1.470 | — | — | — | — | |
| Swalwell et al. [27, 28] | 0021 | 2.7 | 90° | 0.93 | 1.55 | 0.105 | 0.151 | Yes | Yes |
| Reynolds number based on chord length and free-stream velocity, | |
| time-averaged lift and drag coefficients at α = 60° | |
| standard deviation of lift and drag coefficients | |
| Spec | force spectra available? |
| surface pressure distribution available? |
The choice of primary specific test case for this UFR is therefore the flow around a NACA0021 profile at Re = 2.7×105, α = 60° and with a spanwise domain size of Lz = 4c. The justification for this choice is given by the above reviews of previous computational and experimental studies:
- A significant degree of scatter in the mean force coefficients is apparent between facilities, e.g. 12% for at α = 60° (Table 1) and information about the relative fidelity of the experiments is absent. Therefore the experiment with the richest data is chosen (see previous point).
- Although it would be desirable to choose an experiment that has been conducted primarily for the validation of CFD, this is not the case for any of the available experiments.
- A large body of computational data is available for the chosen case, which in contrast to the experiments exhibits a low degree of scatter. This data is taken from recognised international comparison exercises with a rich variety of turbulence models assessed, good quality control, and systematic investigation of the principal test case uncertainties.
- In addition to the primary NACA0021 test case, earlier results from the NACA0012 test case will be drawn upon to increase the richness of the best practice advice (BPA). This is justifiable because of experimental evidence that the effects of Reynolds number and profile thickness are negligible in the range 25° < α < 180° [20].
Contributed by: Charles Mockett; Michael Strelets — Upstream CFD GmbH, Berlin; New Technologies and Services LLC (NTS) and St.-Petersburg State Polytechnic University
© copyright ERCOFTAC 2024





![{\displaystyle {\sigma \left[C_{l}\right]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/171852e2c01696596f14c752822779fb6f9abe8c)
![{\displaystyle {\sigma \left[C_{d}\right]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9533295f97012fb3376cde634755e291793b033d)



![{\displaystyle {\sigma \left[C_{l}\right],\sigma \left[C_{d}\right]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6c65b2dadb3a4054239ac9006f2f945db210c1c2)