AC 6-07 Evaluation
Draft tube
Application Challenge 6-07 © copyright ERCOFTAC 2004
Evaluation
Comparison of CFD Results and Test data
Both workshops used (r) as BC but (n) is currently the most complete test case. It is therefore recommended that future calculations use the (n)-set of data for each case for comparisons with the experiments. However, if the purpose is e.g. to validate a new code or for some other reason compare with other computations the (r)-set of data is still recommended.
Thus, data presented here are all based on computations using the (r) inlet boundary condition for both the T test case and the R test case. Comparison of CFD with test data may be qualitative (e.g. scatter plots, contour plot comparison) or quantitative (statistical measures, e.g. mean bias and variance). Particular focus is given to comparisons between measured and calculated [../../help/glossary.htm DOAP]s. All data discussed here are available in the Proc-W2.
Engineering Quantities and DOAP:s
The results on engineering quantities, calculated by the contributors themselves, for both the T and the R test cases, are presented in Table 4.1.
In Table 4.2. is presented the engineering quantities for all computations, evaluated in a uniform way as described in Proc-W2, Appendix C1. Table 4.3 shows the major design and assessment parameters DOAPs from experiment and simulations. Figure 4.1 present the results in graphical form.</nowiki>
Discussion
A comparison between results in Tables 4.1 and 4.2 shows immediately, in some cases, large difference in computed results, depending on how the engineering parameters are estimated (how extrapolation to the wall is carried out, etc.), and the code used. This is particularly important for Cpr,wall and ζ.
It is also clear that there is a large difference between computed Cpr,wall and Cpr,average. The reason for this latter discrepancy is the following: Radial pressure distributions, experimentally determined and computedcurves, in CSIa, were shown in Proc.T99W2, Part2, pp.55-58. For the experimental profile, see also Andersson (2003b), fig.19.
An analysis of these figures clarifies the main reason for the large values of Cpr,wall, and also for the large scatter in Cpr,wall:
The computed radial pressure distributions generally fall of sharply near the outer wall whereas the experimental distributions exhibit a sharp rise in pressure in this region, followed by a very small decrease just at the wall. The computed wall pressures at CSIa are therefore much lower than the average pressure over the same cross-section. Cp,wall is thus dominated by the wall-value, which is not representative for the average pressure. Using the average or average pressure over the inlet cross-section therefore gives a much more representative (and lower) Cpr, as shown in Table 4.2. (generally Cpr,wall is 1.14-1.66, and Cpr,average is 0.89-0.99).
The main reason for this difference in radial pressure distribution is that the grid in this region is not fine enough and that it does not represent the true surface geometry sufficiently accurate. Evidence of this can be found in Proc.T99W2, paper by Jonzén et al. (2003), Table 2, where a much finer grid than the standard grid recommended by the organizers, gave a difference in Cpr,wallof -0.12, that is, a 10 % decease in Cpr,wall. So, in spite of the relatively fine grid that was proposed by the organizer, it is found that this grid is still too coarse, particularly near the inlet.
For the remaining discussion we will focus on the results of Table 4.3 and Figure 4.1, which show the major design or assessment parameters taken from computations (recalculated by the organizers) and the corresponding experimental values.
It is clear that the scatter in computed Cpr,average is much smaller than in Cpr,wall. This fact, together with the discussion above, shows that Cpr,average is a much more suitable DOAP than Cpr,wall. Table 4.3 also shows that the computed values of Cpr,average are lower than the experimentally determined value, the difference being larger that the estimated uncertainty. Thus, the difference is significant. The reason for this discrepancy is discussed further in section 4.2.1.
From Table 4.3 and Figure 4.1 one can also see that the computed energy-loss coefficient (ζ) shows a surprisingly large scatter and also that the experimental value has a very large uncertainty, Andersson, (2003a). There are several reasons for the large scatter in (ζ): It is an ill-conditioned quantity since it comes out as the difference between two (almost equal) large numbers, (see eq. 9) and the uncertainty in Cp thus has a large effect on (ζ). The experimental value also has a large uncertainty, mainly for the same reason. Also, quantities which could not be measured are determined as a best estimate from the computed result. So, in spite of the effort made, it seems to be very difficult to obtain an accurate experimental determination of (ζ).
Table 4.1 Engineering quantities, calculated by the contributors. (from Proc.T99W2, part 2, p.5)
|
ACRONYM |
Remark | ||||||||||
|
CASE T |
Cp |
|
|
|
|
|
|
|
|
|
|
|
AEAT keps |
1,1300 |
0,0830 |
1,0180 |
1,1700 |
0,0690 |
0,0640 |
1,0760 |
1,1250 |
0,0460 |
0,0430 |
|
|
CKD keps |
1,1606 |
0,1044 |
0,9986 |
1,1702 |
0,0588 |
0,0121 |
1,0602 |
1,1089 |
0,1865 |
0,0605 |
|
|
HQ-FIDAP keps |
1,7460 |
0,1050 |
1,0300 |
1,3150 |
0,0560 |
0,0270 |
1,0800 |
1,1470 |
0,2920 |
-0,0870 |
|
|
HQ-FINE keps |
1,1040 |
0,1590 |
1,0300 |
1,0900 |
0,0560 |
0,0500 |
1,0800 |
1,1360 |
0,2930 |
-0,1290 |
|
|
HQ-TASC keps |
1,3940 |
0,0910 |
1,0300 |
1,2220 |
0,0560 |
0,0490 |
1,0800 |
1,1400 |
0,2920 |
-0,1320 |
|
|
HTC keps |
1,2500 |
0,1250 |
1,0260 |
1,4620 |
0,0670 |
0,0410 |
1,0770 |
1,2140 |
0,2860 |
0,1080 |
|
|
NUT keps |
1,2730 |
0,0690 |
1,0100 |
1,2520 |
0,0590 |
0,0190 |
1,0720 |
1,1240 |
0,3070 |
0,0800 |
|
|
TEV keps |
1,2330 |
0,1410 |
1,0040 |
1,2180 |
0,0570 |
0,0740 |
1,0540 |
1,1110 |
0,3020 |
0,2570 |
|
|
VUAB keps |
1,2946 |
0,0870 |
1,0239 |
1,2360 |
0,0580 |
0,0091 |
1,0771 |
1,1029 |
0,3024 |
-0,2018 |
Values are from recalculation by F. Engström. |
|
LTU keps |
1,2880 |
0,0570 |
1,0381 |
1,2226 |
0,0596 |
0,0594 |
1,0889 |
1,2244 |
0,1772 |
0,1506 |
Corrected value for Cp wall |
|
Iowa keps |
1,1950 |
||||||||||
|
Experiment T |
1,120 |
0,09 |
1,040 |
1,090 |
0,060 |
0,040 |
1,110 |
1,020 |
0,310 |
αsw III, without vertical comp. | |
|
β III, only axial comp. | |||||||||||
|
CASE R |
|
|
|
|
|
|
|
|
|
|
|
|
CKD realizable-keps 2 |
1,1608 |
0,1047 |
0,9980 |
1,1475 |
0,0299 |
0,0075 |
1,0327 |
1,0849 |
0,1034 |
0,0333 |
|
|
HQ-FIDAP keps 2 |
1,7980 |
0,0920 |
1,0280 |
1,1940 |
0,0290 |
0,0190 |
1,0520 |
1,0920 |
0,1570 |
-0,0680 |
|
|
HQ-FINE keps 2 |
1,1200 |
0,1690 |
1,0270 |
1,2220 |
0,0280 |
0,0330 |
1,0510 |
1,1210 |
0,1570 |
-0,0450 |
|
|
HQ-TASC keps 2 |
1,4050 |
0,0920 |
1,0280 |
1,2090 |
0,0290 |
0,0450 |
1,0520 |
1,1260 |
0,1570 |
-0,0620 |
|
|
HTC cubic-keps 2 |
0,9950 |
0,2050 |
1,0240 |
1,4750 |
0,0390 |
0,0300 |
1,0480 |
1,2160 |
0,2370 |
0,0610 |
|
|
HTC quadratic-keps 2 |
0,9510 |
0,2480 |
1,0240 |
1,4500 |
0,0390 |
0,0390 |
1,0480 |
1,2200 |
0,2370 |
0,0490 |
|
|
NUT keps 2 |
1,0750 |
0,0700 |
1,0080 |
1,3540 |
0,0290 |
0,0260 |
1,0400 |
1,1820 |
0,1640 |
0,0850 |
|
|
TEV rsm 2 |
1,2080 |
0,1250 |
1,0030 |
1,2930 |
0,0280 |
0,0130 |
1,0300 |
1,1230 |
0,1630 |
0,0250 |
|
|
VUAB keps 2 |
Resimulated after workshop, no data available | ||||||||||
|
LTU keps 2 |
1,3971 |
0,0586 |
1,0332 |
1,1875 |
0,0307 |
0,0524 |
1,0584 |
1,1487 |
0,0964 |
0,0879 |
|
|
Iowa keps 2 |
1,2365 |
different ε | |||||||||
|
Iowa komega 2 |
1,2273 |
different ε | |||||||||
|
VUAB keps 3 |
Resimulated after workshop, no data available | ||||||||||
|
CKD rsm 3 |
1,0420 |
0,1230 |
0,9854 |
1,2531 |
0,0291 |
0,0074 |
1,0195 |
1,1332 |
0,1024 |
0,0009 |
|
|
EXA vl 3 |
1,1880 |
0,1480 |
1,0100 |
1,2360 |
0,0280 |
0,0450 |
1,0000 |
1,0840 |
0,0950 |
||
|
HTC LES 3 |
0,9370 |
0,2170 |
1,0850 |
1,8000 |
0,0470 |
0,0900 |
1,1080 |
1,3700 |
0,2600 |
0,0700 |
|
|
NUT LES 3 |
1,0900 |
1,0080 |
1,1630 |
0,0290 |
1,0400 |
1,1210 |
0,1640 |
||||
|
Experiment R |
1,09 |
1,040 |
0,030 |
1,080 |
0,170 |
Table 4.2. Engineering quantities, recalculated by the organizers (from Proc.T99W2, part 2, p. 17)
|
ACRONYM |
Remark | |||||||||||
|
CASE T |
|
|
|
|
|
|
|
|
|
|
|
|
|
AEAT |
1,361 |
0,952 |
0,150 |
1,038 |
1,210 |
0,059 |
0,036 |
1,093 |
1,140 |
0,302 |
-0,087 |
|
|
NUT |
1,262 |
0,925 |
0,043 |
1,023 |
1,234 |
0,059 |
0,010 |
1,079 |
1,104 |
0,308 |
-0,227 |
|
|
TEV |
1,276 |
0,963 |
0,050 |
1,024 |
1,201 |
0,058 |
0,025 |
1,077 |
1,119 |
0,301 |
-0,131 |
|
|
HTC |
1,250 |
0,916 |
0,172 |
1,042 |
1,270 |
0,056 |
0,009 |
1,091 |
1,117 |
0,293 |
-0,205 |
|
|
VUAB |
1,295 |
0,917 |
0,087 |
1,024 |
1,236 |
0,058 |
0,009 |
1,077 |
1,103 |
0,302 |
-0,202 |
|
|
CKD |
1,185 |
0,892 |
0,110 |
1,019 |
1,276 |
0,059 |
0,009 |
1,076 |
1,119 |
0,305 |
-0,252 |
|
|
HQ-FIDAP |
1,665 |
0,921 |
0,120 |
1,037 |
1,325 |
0,056 |
0,016 |
1,089 |
1,152 |
0,292 |
-0,105 |
|
|
HQ-FINE |
1,144 |
0,991 |
0,077 |
1,037 |
1,219 |
0,056 |
0,034 |
1,088 |
1,142 |
0,293 |
-0,094 |
|
|
HQ-TASC |
1,397 |
0,956 |
0,152 |
1,037 |
1,230 |
0,056 |
0,035 |
1,089 |
1,145 |
0,292 |
-0,145 |
|
|
Iowa |
1,195 |
0,887 |
0,162 |
1,037 |
1,347 |
0,059 |
0,011 |
1,093 |
1,151 |
0,302 |
-0,108 |
|
|
LTU |
1,537 |
0,980 |
0,066 |
1,034 |
1,144 |
0,059 |
0,030 |
1,082 |
1,106 |
0,302 |
-0,037 |
|
|
CASE T |
|
|
|
|
|
|
|
|
|
|
|
|
|
AEAT |
0,145 |
0,520 |
1,065 |
0,519 |
0,513 |
0,511 |
0,989 |
0,984 |
1,107 |
1,277 |
2,308 |
|
|
NUT |
0,145 |
0,518 |
1,064 |
0,503 |
0,509 |
0,511 |
1,013 |
1,017 |
1,094 |
1,257 |
2,888 |
|
|
TEV |
0,145 |
0,520 |
1,064 |
0,515 |
0,517 |
0,518 |
1,004 |
1,006 |
1,092 |
1,251 |
2,516 |
|
|
HTC |
0,145 |
0,520 |
1,065 |
0,518 |
0,515 |
0,512 |
0,993 |
0,988 |
1,107 |
1,292 |
3,022 |
|
|
VUAB |
0,145 |
0,522 |
1,064 |
0,514 |
0,516 |
0,517 |
1,005 |
1,007 |
1,092 |
1,258 |
2,842 |
|
|
CKD |
0,145 |
0,520 |
1,064 |
0,509 |
0,510 |
0,510 |
1,002 |
1,003 |
1,089 |
1,295 |
3,343 |
|
|
HQ-FIDAP |
0,145 |
0,521 |
1,064 |
0,522 |
0,522 |
0,522 |
1,000 |
0,999 |
1,102 |
1,366 |
3,730 |
|
|
HQ-FINE |
0,145 |
0,521 |
1,064 |
0,521 |
0,522 |
0,517 |
1,001 |
0,991 |
1,102 |
1,285 |
3,235 |
|
|
HQ-TASC |
0,145 |
0,521 |
1,064 |
0,522 |
0,516 |
0,515 |
0,989 |
0,986 |
1,102 |
1,294 |
2,487 |
|
|
Iowa |
0,145 |
0,520 |
1,064 |
0,509 |
0,508 |
0,506 |
0,999 |
0,994 |
1,106 |
1,381 |
3,049 |
|
|
LTU |
0,145 |
0,520 |
1,065 |
0,516 |
0,519 |
0,518 |
1,005 |
1,003 |
1,103 |
1,200 |
1,967 |
Table 4.3. Major design and assessment parameters (DOAPs).
|
CASE T |
|
|
|
|
AEAT |
|
|
|
|
NUT |
|
|
|
|
TEV |
|
|
|
|
HTC |
|
|
|
|
VUAB |
|
|
|
|
CKD |
|
|
|
|
HQ-FIDAP |
|
|
|
|
HQ-FINE |
|
|
|
|
HQ-TASC |
|
|
|
|
Iowa |
|
|
|
|
LTU |
|
|
|
|
Experiment T |
1,12 + 0,02 - 0,01 |
1.06 + 0,04 - 0,02 |
0,09 + 0,06 |
Figure 4.1 Major design and assessment parameters
Velocity Field
Table 4.4 shows differences in results between calculations and experiments in CS II and III. Briefly, two fields (e.g. U-velocity), one field obtained from experiments and the other one obtained from computations, are compared on the same grid, and the standard deviation or RMS value and Mean value, Max and Minimum values are computed. By this method, we get a comparison of the whole field and also a quantitative measure of the difference between the fields (the Stdv).

Figure 4.2. Normalised axial velocity at the horizontal mid-plane of CS II. (-Mean value of CFD-calculations T99 W2; : Max /min value from CFD simulations T99 W2; + VUAB CFD simulation; x Experiment)
In Figure 4.2 one can see that there is a rather good agreement between the different CFD-calculations for test case T, comparing the (normalised) axial velocity. The mean variation is ± 0.04 for the CFD-calculations at each point of the mid-plane of the calculations. However, in the worst regions the differences are as high as ± 0.15. The results from VUAB (+) is also included, to show how a single computation behaves along the profile. Compared with Experiments (x), there is a significant difference in the resulting profile, that cannot be explained by the variation between CFD-calculations or experimental uncertainties.
An illustrative way of showing the accuracy of the simulations relative to the measured veloctiy values is shown in Figure 4.3 where the difference between the simulations and the experiments are shown. The difference is defined as Uexp/Uexp, average − Usim/Usim,average
|
Figure 4.3: Difference plot of the axial velocity at cross section II. From Cervantes & Engström |
In Proc-W2, Appendix C2 are collected the difference plots for some selected simulations. It is seen that the general feature of two minima are similarly determined among the contributions, and that the maximum deviations are large (30%).
An quantitative integral measure of the accuracy of these calculations can be defined as the standard deviation of the data integrated over the cross section. The result of such calculations is collected in Figure 4.4 and in Table 4.4.
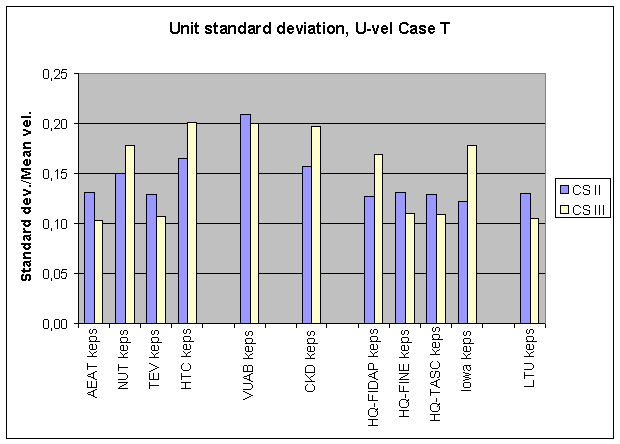 Figure 4.4: Standard deviation of velocity difference integrated over cross sections II and III.
Figure 4.4: Standard deviation of velocity difference integrated over cross sections II and III.
Table 4.4 Comparisons between computations and experiments at CS II and III
Discussion of Scatter in Design or Assessment Parameters
and ζ)
In the results collected, it is noticed that the two key engineering quantities, Cp and ζ, are subject to considerable scatter among the contributions. Part of the scatter is due to the post-processing of data, but other factors also contribute, as will be discussed here.
From the figures of the radial pressure distribution at section Ia (Figure 3 in Proc-W2) the reason for the large values of Cp,wall, and also its large scatter, is explained by the observation that the computed radial pressure distributions generally fall off sharply near the outer wall, whereas the experimental distribution show a sharp rise in this region, followed by a small decrease as the wall is approached. The computed wall pressure levels at CS Ia are therefore much lower than the average pressure over the same cross-section. Using the average pressure over the inlet cross-section therefore gives a more representative (and lower) value of Cp. (Cp,wall is in the range 1.14 -1.66 and Cp,average in the range 0.89-0.99).
An explanation for the scatter in the radial pressure distribution at CS Ia may be that the grid in this region is not fine enough to resolve the rapid evolution of the pressure and that it does not represent the surface geometry accurately enough. From the (inviscid) equation for the radial pressure,
it is noticed that a large contribution to the radial pressure gradient comes from the second term even in regions where the streamwise gradient is moderate because of the magnitude of uax. A finer resolution of this region may result in a 10% reduction of the Cp,wall-value as demonstrated by Jonzén et al.
The scatter in the loss coefficient may be due to at least two reasons. In the expression for ζ, (9), the last term is close to unity, and the second is small (the area ratio is small) which means that the evaluation of ζ is ill-conditioned despite the accuracy in Cp'. This indicates that the use of ζ as a key parameter to evaluate gains in efficiency from e.g. a geometry optimisation may be risky unless a reconditioning of the calculations can be done. To validate such a gain experimentally, may be even more difficult since not all of the α-values are available experimentally. From the experimental results it has been deduced that ζ = 0.09 (+0.06/-0.07) which illustrates the difficulty encountered in this evaluation.
A second source of uncertainty in ζ emanates from the use of wall-functions for the near-wall calculations. Since it is expected that most flow losses occur in this region, and in fact will be reflected in the pressure results, a more careful evaluation based on the energetics associated with the wall functions could be recommended as a separate method to determine ζ. A further factor adding to the losses is also the periodic character of the flow, most notable at the runner.
Conclusions and Recommendations
The most important results and suggestions of the workshop are summarised below.
• The 700k computational grid suggested by the organisers turns out to be too coarse, particularly near the inlet section, where it has a large effect on computed pressure recovery Cp,wall . This is caused by the fact that the pressure gradients in both the axial and radial directions are large and must be resolved properly.
• The uncertainty in the experimentally determined energy-loss factor is large because it is an ill-conditioned quantity, to a large extent determined by Cp.
• It was found that the y+ criterion for wall functions was violated in many regions of the flow.
• The importance of complete and well-defined inlet boundary conditions is highlighted in many of the workshop contributions.
• The pressure recovery coefficient Cp,average , based on the average pressure over the inlet cross-section, is a suitable assessment parameter, which for Case T is calculated with a scatter of about + 5%. The difference between computed and experimentally determined Cp,average, is statistically significant.
• Computations of Case T by different groups but with the same mesh, inlet- and outlet boundary conditions, and turbulence model, generally give very similar results. Thus, the “Quality” in the concept of “Quality and Trust”, is not too far away.
• Because of the abovementioned weaknesses, it has, so far, not been possible to draw conclusions about the influence of turbulence model on the solution.
Suggestions for further computational and experimental work are given below:
• For further computational work, as a first step, a much finer grid must be constructed, particularly near the inlet. This is necessary also when using wall functions.
• As step 2, it is recommended that the wall functions should be replaced by suitable near-wall models.
• Since more than 80 % of the pressure recovery takes place in the first 10 % or so of the draft tube length (the draft tube cone), more detailed (axial and radial) pressure and velocity measurements are required.
• Also, complete 3-component velocity measurements in some cross sections are highly desirable.
These suggestions are directed towards increasing the quality of the computed solutions and increasing the accuracy of the experimentally determined engineering parameters, thus increasing the value and usefulness of the draft tube test case.
References
Bergström, J. (2000). “Modeling and Numerical Simulation of Hydro Power Flows”. Doctoral Thesis 2000-06, Luleå University of Technology, Department of Mechanical Engineering, Division of Fluid Mechanics.
Casey M. & Wintergerste T. (editors). (2000) ERCOFTAC Best Practice Guidelines. ERCOFTAC Special Interest Group on “Quality and Trust in Industrial CFD”.
Gebart B.R., Gustavsson L.H. & Karlsson R.I. (editors) (2000a) “Turbine 99 – Workshop on Draft Tube Flow”. Technical Report 2000-11, Luleå University of Technology, Department of Mechanical Engineering, Division of Fluid Mechanics. ISSN:1402-1536
Gebart B.R., Gustavsson L.H. & Karlsson R.I. (2000b) “Report from Turbine 99 – Workshop on Draft Tube Flow in Porjus, Sweden, 20-23 June 1999”. Paper presented at the 20th IAHR Symposium Hydraulic Machinery and Systems. Aug. 6-9, 2000, Charlotte, North Carolina, U.S.A.
Engström T.F., Gustavsson L.H. & Karlsson R.I. (2002) “Report from Turbine 99 – Workshop 2 on Draft Tube Flow”. The second ERCOFTAC Workshop on Draft Tube Flow, held in Älvkarleby, Sweden, June 18-20, 2001. Paper presented at the 21st IAHR Symposium Hydraulic Machinery and Systems, Lausanne, Switzerland, Sept. 2002
Engström, T.F., Gustavsson, L.H., & Karlsson, R.I. (2003), Proceedings of Turbine-99 - Workshop 2. The second ERCOFTAC Workshop on Draft Tube Flow. Älvkarleby, Sweden, June 18-20 2001. http://epubl.luth.se/1402-1536/2000/11/index-en.html.
Andersson U. (2003a) Turbine 99 – Experiments On Draft Tube Flow (Test Case R) In: Proceedings from Turbine 99 – Workshop 2, Engström et al. (editors) (2003).
Andersson U. (2003b) Test Case T – some new results and updates since Workshop I. In: Proceedings from Turbine 99 – Workshop 2, Engström et al. (editors) (2003).
Jonzén S, Hemström B, Andersson U (2003) “Turbine 99- Accuracy in CFD simulations on draft tube flow” (2003). In Proceedings from Turbune 99 – Workshop 2, Engström et al. (editors) (2003).
© copyright ERCOFTAC 2004
|
Contributors: Rolf Karlsson - Vattenfall Utveckling AB
|


