Flow and heat transfer in a pin-fin array

Confined Flows

Underlying Flow Regime 4-18

Test Case Study

Brief Description of the Study Test Case

This should:

Convey the general set up of the test-case configuration( e.g. airflow over a bump on the floor of a wind tunnel)
Describe the geometry, illustrated with a sketch
Specify the flow parameters which define the flow regime (e.g. Reynolds number, Rayleigh number, angle of incidence etc.)
Give the principal measured quantities (i.e. assessment quantities) by which the success or failure of CFD calculations are to be judged. These quantities should include global parameters but also the distributions of mean and turbulence quantities.

The description can be kept fairly short if a link can be made to a data base where details are given. For other cases a more detailed, fully self-contained description should be provided.

The experiments from Ames et al. deal with the flow of air around 8 staggered rows of 7.5 heated pins, spaced at P=2.5D in both stream-wise and span-wise directions (based on center to center distances). The diameter of the pins is set to 0.0254 m (1 inch) and the channel height is twice the diameter (H=2D). The Reynolds numbers $Re_{D}$ based on the pin diameter and the average gap bulk velocity which have been tested are equal to 3,000, 10,000 and 30,000, respectively. The gap bulk velocity is determined between two adjacent pins of the same row. Taking $V_{0}$ and $V_{G}$ as the inlet and gap velocities, respectively, and considering mass conservation, one obtains $V_{G}=P/(P-D)V_{0}$ .

A sketch of the original experimental configuration is given in Figure 1. In the experiment, the distance between the inlet (beginning of the test section; end of a converging nozzle) and the center of the first cylinders is equal to 7.75D. The distance between the center of the last cylinders and the test section is also equal to 7.75D.

The bottom wall is heated with a constant heat-flux whereas the other walls are adiabatic (Ames et al.). All the flow properties can be taken constant, the Prantl number is equal to 0.71.

Figure 1: Sketch of Ames et al. experiment

Test Case Experiments

Provide a brief description of the test facility, together with the measurement techniques used. Indicate what quantities were measured and where.

Discuss the quality of the data and the accuracy of the measurements. It is recognized that the depth and extent of this discussion is dependent upon the amount and quality of information provided in the source documents. However, it should seek to address:

How close is the flow to the target/design flow (e.g. if the flow is supposed to be two-dimensional, how well is this condition satisfied)?

Estimation of the accuracy of measured quantities arising from given measurement technique

Checks on global conservation of physically conserved quantities, momentum, energy etc.

Consistency in the measurements of different quantities.

Discuss how well conditions at boundaries of the flow such as inflow, outflow, walls, far fields, free surface are provided or could be reasonably estimated in order to facilitate CFD calculations

Experimental Setup

General Description

The description given in the present section has been given by F. Ames during the $15^{th}$ Ercoftac SIG15 Workshop. More information could also be found in Ames et al. (2004, 2005, 2006, 2007). The objective of the experiments was to create a database that includes heat transfer distributions on the pin fins and endwall, pressure distributions on the pin fins and endwall, documentation of turbulence intensities and scales, and measurements of turbulence and velocity distributions across the channels. The research was conducted in a small bench top wind tunnel (see Figure 2) which included a small blower capable of producing a flow of $0.3m^{3}/s$ at a static pressure rise of 2000 Pa. The pin fin array was designed in an 8 row, 7 1/2 pin per row staggered arrangement. Both the cross passage (S/D) and streamwise (X/D) pin spacing were equal to 2.5 while the pin height to diameter (H/D) was 2. The pin diameter was chosen to be equal to 2.54 cm. The flow conditioning system first spreads out the flow from the blower to the width of the array using a two-stage multi-vane diffuser. A heat exchanger was installed in the system downstream from the diffuser to control the tunnel temperature in order to impose a constant value. The heat exchanger discharges the flow into a screen box consisting of three nylon window screens to reduce the cross stream velocity variations in the flow. Directly downstream of the screens, the flow enters a smooth 2.5 to 1 area ratio nozzle prior to entering the test section. The pin fin array test section begins 7.75 D upstream of the centerline of the first row of pins and ended 7.75 D downstream of the centerline of the last row of pins. The inlet total temperature and pressure and static pressures were measured 5 D upstream from the row 1 centerline and the exit static pressures were measured 5 D downstream from row 8. Downstream from the test section the flow was directed through a 90° rectangular elbow then a rectangular channel followed by a second 90° elbow before entering a 20.8 cm diameter orifice tube used to measure the array flow rate. Tests were conducted at three Reynolds numbers : 3 000, 10 000, and 30 000. The Reynolds number is based on the maximum velocity (also called the gap velocity $V_{G}$ , see the previous section). Fluid properties were determined from the inlet conditions.

The remaining description will focus on the data which are used in the present work, the heat transfer and pressure distributions on the pins and the endwalls, respectively, are not included.

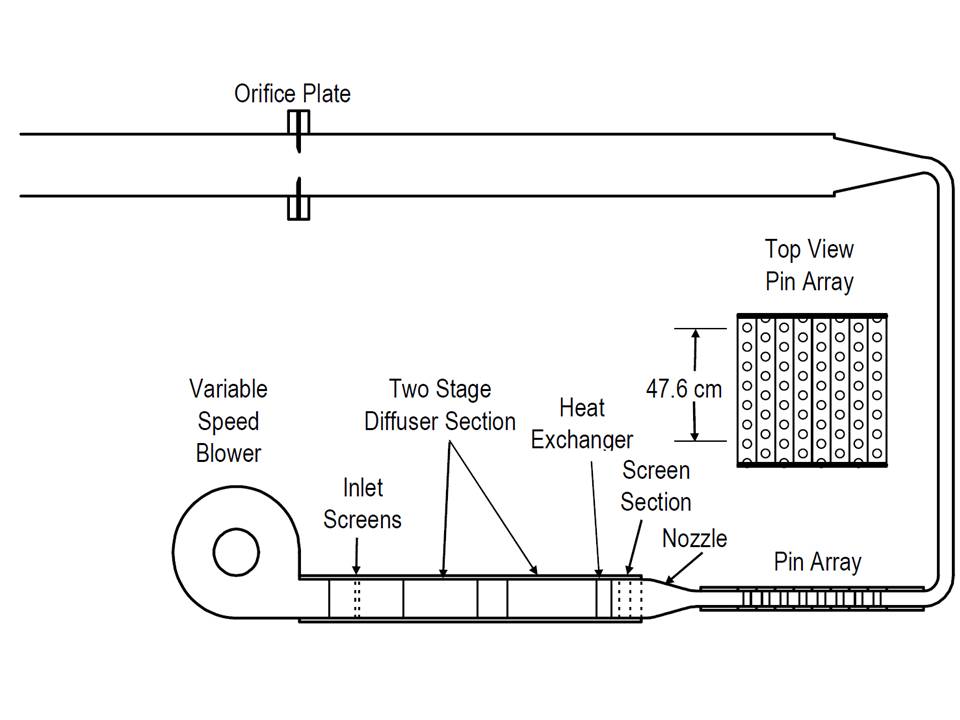
Figure 2: Sketch of Ames et al. experimental loop (image taken from Ames et al. (2007)

Pin fin surface static pressure

The initial research focus involved measuring the pin midspan surface static pressure distribution and heat transfer. The midspan pressure distributions were acquired using a 2.54 cm diameter pin which contained 20 equally spaced 0.76 mm static pressure taps around the midspan perimeter. Measurements were made in 6° increments by indexing the pin. The pin midspan heat transfer was acquired using a 2.54 cm diameter epoxy pin with 24 fine wire thermocouples with junctions cast near the surface at the midspan of the pin. The pin was wrapped with a 0.023 mm Inconel foil backed with a 0.13 mm Kapton film and adhered to the pin using a pressure sensitive acrylic adhesive which was 0.05 mm thick. One bus bar was soldered to the foil while the other was adhered using electrically conductive silver epoxy with the bus bars integrated into the back surface of the pin. The constant heat flux boundary condition was generated by passing a large DC current, measured using a constantan shunt resistor, through the foil. During heat transfer measurements, the pin was indexed at 5° increments to develop better surface heat transfer resolution. Additionally, the pin was also rotated to allow measurement of the pin backside heat transfer. The surface heat flux was taken as the dissipated heat flux plus any positive or negative contribution due to conduction less the thermal radiation. Conduction through the pin was estimated using a finite difference model of the pin. The surface temperatures were determined based on the measured temperatures extrapolated to the surface of the foil based on the local heat flux and conductance from the junction to the foil surface. The emissivity of the foil was assumed to be 0.21

 Pin  fin array turbulence and velocity measurements.   Array  turbulence and velocity

measurements were acquired using single and X wire hotwire probes powered by a TSI IFA 300 constant temperature anemometry unit. A special low velocity jet was developed to calibrate the wires from 0.4 m/s through 40 m/s to enable measurements of turbulence and velocity distributions over a 10 to 1 range in Reynolds number. The hotwires were positioned in the channel between two pins using a two axis traversing system configured from two lead screw drive tables for actuating the probe in the cross-passage and endwall normal directions. Turbulence measurements to document the streamwise development of turbulence intensity, dissipation, and turbulent scale were acquired for each row in a plane defined in connecting adjacent pin centerlines at the positions shown in Figure 2a and averaged. Velocity and turbulence distributions off the endwall and off the pin were acquired along the positions shown in Figure 2b. Turbulence measurements to document the turbulence dissipation and scale were based on 40 velocity time records containing 8192 points and were sampled at 5, 15 and 40 kHz. Each record was used to generate a power spectrum using an FFT and then averaged. The local dissipation was determine by fitting the inertial subrange of the averaged power spectrum to Eq. (3-152a) of Hinze [20] taking A as 1.62 after Ames and Moffat [21]. The integral length scale was estimated using Taylors hypothesis by multiplying the integral time scale by the local convective velocity. The integral time scale was determined by integrating the autocorrelation in time to its first zero crossing. The autocorrelation in time was determined from an inverse FFT of the averaged power spectrum.

 Pin  and  endwall  static  pressure  distributions.  Pin  fin  and  endwall  surface  pressure

measurements were acquired using a 8.65 cm diameter plug with 20 taps. The plug had 10 taps on the endwall spaced radially outward from the pin and 10 taps on the pin as shown in Figure 3a. The pin was rotated at 10° increments to document the pin and endwall surface pressure distribution as shown in Figure 3b. The actual tap locations are given in the legend on Figure 3b. The plug with rotating pressure taps fit in 8 alternating holes in the top of a special test surface corresponding to positions in rows 1 through 8. Note that the pressure measurements were assumed to be symmetric in the cross-passage direction. These pressure distributions were reported in Ames and Dvorak [4] but were not included here. Endwall heat transfer measurements. Full surface endwall heat transfer measurements were acquired using a constant heat flux test surface shown in Figure 4 and a FLIR SC500 IR camera. A constant surface heat flux boundary condition was generated using three, 15.28 cm wide by 68.58 cm long, 0.023 mm thick Inconel foils with 0.127 mm thick Kapton backing and 0.05 mm thick acrylic adhesive. The three foils were adhered to a 0.89 mm thick sheet of fiberglass epoxy board which in turn was epoxied to a 3.81 cm thick section of isocyanurate foam. The three foils were connected in series. The current through the foil and the voltage across the center foil was used to determine the surface heat flux. The surface heat flux was corrected for both local radiation and conduction loss. The radiation loss assumed the emissivity of the surface was 0.96 and the conduction loss was based on a simple 1-D model. The constant heat flux which was generated under the pins was conducted away using an aluminum cooling plate with 56-2.54 cm diameter aluminum pins. The top of the aluminum pins were located just under the fiberglass epoxy board and aligned with the acrylic pins which covered the foil within the test section. The aluminum cooling plate was controlled to a temperature that minimized the influence of the leading edge or trailing edge temperature boundary condition of the foil. However, since the surface heat transfer varied around the pin surface, this produced a mismatch that occurred between the upstream and downstream heat transfer image of the endwall around a pin. This interface area between to two images was averaged and smoothed locally assuming the average of the two values at the interface was closer to the actual value. The difference between the average value and a given image interface was part of the experimental uncertainty.

 The  key  to  accurate  full  surface  endwall  heat  transfer  measurements  is  the  ability  to

measure the surface temperature accurately. Full surface heat transfer measurements were acquired using a FLIR SC500 Infrared Camera. The camera was equipped with a special lens which allowed a much wider angle (45°) and a much closer focal plane (6.35 cm) than the standard lens. This allowed the camera to acquire a 130 by 260 pixel image (3.175 cm by 6.35 cm) through a 5.08 cm diameter zinc selenide window. At each measurement location, the camera location was indexed on the pins to ensure a consistent camera location for all the measurements. The accuracy of the surface temperature measurement was enhanced by the calibration of the camera on a calibration surface through the same zinc selenide window, the manual resetting of the camera every three or four pictures, and the averaging of 9 images for each heat transfer realization. The driving force temperature difference was calculated as heated endwall surface temperature corrected for the inlet temperature during the test and for the local calibration less the unheated endwall surface temperature corrected for the inlet temperature and the local calibration. The temperature difference also accounted for the bulk temperature rise of the air due to endwall heating. The combination of these methods reduced the uncertainty band of the surface temperature measurement from about +/-2 °C to about +/- 0.7 °C. Data Uncertainties. Uncertainties in the reported values were estimated based on the root sum square method described by Moffat [22]. The uncertainty in the reported Reynolds number was determined to be +/- 3% due to the possible error in the flow rate measurement. Pin midspan heat transfer was reported in terms of NuD/ReD 1/2. The worst case uncertainty in midspan NuD/ReD 1/2 was estimated to be +/- 6%. The largest uncertainty for the midspan pressure coefficient was estimated to be +/- 0.075 due to the very low dynamic pressure at the low Reynolds number condition. However, the uncertainty in the pressure coefficient was no more than +/- 0.025 at the higher two Reynolds numbers. Uncertainty in the measurement of velocity using a hot wire was estimated to be +/- 3% except in the near wall region where positional and conduction effects could substantially increase the possible error. Additionally, at high turbulence levels single wire velocities can be significantly overestimated if traverse fluctuation velocities, normal to the wire become high. For example at 30% intensity levels velocities can be overestimated by 4%. The reported value of turbulence intensity had an uncertainty of approximately +/- 3% and the uncertainty in the report of the energy (Lu) and integral (Lx) scales was about +/-13%. Uncertainties in the reporting of pressure coefficients for the full surface pressure measurements are similar to midline pin measurements. However, these values can be significantly higher when positional uncertainties in high pressure gradients are considered. The reported uncertainties in Nusselt number are estimated to be as high at +/- 12%, +/-11.4%, and +/-10.5% for the 3000, 10,000, and 30,000 Reynolds numbers respectively in the endwall regions adjacent to the pins and +/- 9% away from the pin. Uncertainty estimates were determined using a 95% confidence interval. Data Acquisition. Pressures and single point temperature measurements were acquired using a PC based data acquisition system. Voltage signals from pressure transducers, thermocouples, and heaters were scanned using an HP3497A data acquisition unit with an integral voltmeter. The integral voltmeter had 1 mV sensitivity. Thermocouples were connected to the HP3497A through a passive constant temperature junction referenced to an ice bath. p 17 / 228 10

Pressures were acquired using a custom build pressure scanner which included two Rosemont pressure transmitters read in parallel and set to full scale ranges of 125 Pa and 1250 Pa. The most sensitive reading in range was used and the sensors had a reported +/- 0.1% of full scale accuracy. Hotwire measurements were acquired through a high speed data acquisition board used with simultaneous sample and hold for X-wire measurements. The TSI IFA 300 Constant Temperature Anemometry Unit had on board buck, gain, and low-pass filtering.

CFD Methods

Provide an overview of the methods used to analyze the test case. This should describe the codes employed together with the turbulence/physical models examined; the models need not be described in detail if good references are available but the treatment used at the walls should explained. Comment on how well the boundary conditions used replicate the conditions in the test rig, e.g. inflow conditions based on measured data at the rig measurement station or reconstructed based on well-defined estimates and assumptions.

Discuss the quality and accuracy of the CFD calculations. As before, it is recognized that the depth and extent of this discussion is dependent upon the amount and quality of information provided in the source documents. However the following points should be addressed: