UFR 3-12 Evaluation: Difference between revisions
David.Fowler (talk | contribs) mNo edit summary |
m (Dave.Ellacott moved page Silver:UFR 3-12 Evaluation to UFR 3-12 Evaluation over redirect) |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 24: | Line 24: | ||
Fig. 1: Isentropic Mach number distribution along pressure and suction side for different turbulence models | Fig. 1: Isentropic Mach number distribution along pressure and suction side for different turbulence models | ||
The measured and predicted heat transfer coefficient h<sub>t</sub>, which is defined as h<sub>t</sub> = q<sub>w</sub>/(T<sub>0∞</sub> | The measured and predicted heat transfer coefficient h<sub>t</sub>, which is defined as h<sub>t</sub> = q<sub>w</sub>/(T<sub>0∞</sub> − T<sub>w</sub>), along the respective suction and pressure sides of the blade is shown in Figure 2. Significant differences among the various models can be observed here. The original k-ε model strongly over-predicts the heat transfer coefficient, especially on the pressure side towards the trailing edge. The same is reported for the original k-ω model by Medic and Durbin (2002). The levels of the predicted heat transfer by the Kato-Launder formulation or the bound on the turbulent time scale model (T bound) are much closer to the experiments. However, at the leading edge on the suction side h<sub>t</sub> is from both models over 30% too high. The predicted slope towards the trailing edge is steeper than from the measurements. On the other hand, the predictions of h<sub>t</sub> are better on the pressure side. This indicates the sensitivity of these two models (Kato-Launder and T bound) against an adverse pressure gradient. Of all four models considered in Medic (2001), the v<sup>2</sup>-f model yields the best results. This model is the only model which is able to capture the trough on the suction side of the experiments. Medic and Durbin (2002) pointed out, that this characteristic is due to the fact that the v<sup>2</sup>-f model is able to predict a reasonable transition location. However, on the pressure side this model under-predicts the recovery of the heat transfer coefficient towards the trailing edge. This may be caused by the tendency of the model towards relaminarisation of the flow (Medic and Durbin, 2002). | ||
<center>[[Image:U3-12d32_files_image016.gif]]</center> | <center>[[Image:U3-12d32_files_image016.gif]]</center> | ||
| Line 30: | Line 30: | ||
Fig. 2: Heat transfer coefficient h<sub>t</sub> distribution along pressure and suction side for different turbulence models | Fig. 2: Heat transfer coefficient h<sub>t</sub> distribution along pressure and suction side for different turbulence models | ||
The heat transfer coefficient is related to the eddy viscosity, where the latter quantity is a function of the turbulent kinetic energy k. Therefore, the differences of the prediction of h<sub>t</sub> obtained from the different models can be directly linked to k. Figures 3 | The heat transfer coefficient is related to the eddy viscosity, where the latter quantity is a function of the turbulent kinetic energy k. Therefore, the differences of the prediction of h<sub>t</sub> obtained from the different models can be directly linked to k. Figures 3 — 6 show the turbulent kinetic energy distribution predicted by the four considered models. Unfortunately, only computed values of this quantity are presented in Medic and Durbin (2002). | ||
An outstanding feature of these results is that in the centre of the passage the turbulent kinetic energy levels predicted by the original k-ε model (or k-ω model) are about 30 times higher than from the v<sup>2</sup>-f model. Furthermore, the latter model shows a decrease of turbulent intensity in the centre passage in contrast to the former model. | An outstanding feature of these results is that in the centre of the passage the turbulent kinetic energy levels predicted by the original k-ε model (or k-ω model) are about 30 times higher than from the v<sup>2</sup>-f model. Furthermore, the latter model shows a decrease of turbulent intensity in the centre passage in contrast to the former model. | ||
| Line 56: | Line 56: | ||
The results from Medic and Durban (2002) suggest that an improvement of the performance of the standard k-ε or k-ω models is possible by using the v<sup>2</sup>-f model. Other options would be the implementation of a bound on the time scale or modifying the production term in the described manner, i.e. the Kato-Launder modification. | The results from Medic and Durban (2002) suggest that an improvement of the performance of the standard k-ε or k-ω models is possible by using the v<sup>2</sup>-f model. Other options would be the implementation of a bound on the time scale or modifying the production term in the described manner, i.e. the Kato-Launder modification. | ||
As mentioned above, higher order turbulence models may perform better than eddy-viscosity based models but are often not a practical option for many industrial applications. The recommendation is therefore to use | As mentioned above, higher order turbulence models may perform better than eddy-viscosity based models but are often not a practical option for many industrial applications. The recommendation is therefore to use — at least for applications with limited computer resources — models derived from the k-ε or k-ω formulation. Often for industrial purposes not the fine structure of turbulence is of interest, therefore the chosen model should be able to capture the main physical features of the flow field. | ||
<font size="-2" color="#888888">© copyright ERCOFTAC 2004</font><br /> | <font size="-2" color="#888888">© copyright ERCOFTAC 2004</font><br /> | ||
| Line 66: | Line 66: | ||
{{UFR|front=UFR 3-12|description=UFR 3-12 Description|references=UFR 3-12 References|testcase=UFR 3-12 Test Case|evaluation=UFR 3-12 Evaluation|qualityreview=UFR 3-12 Quality Review|bestpractice=UFR 3-12 Best Practice Advice|relatedACs=UFR 3-12 Related ACs}} | {{UFR|front=UFR 3-12|description=UFR 3-12 Description|references=UFR 3-12 References|testcase=UFR 3-12 Test Case|evaluation=UFR 3-12 Evaluation|qualityreview=UFR 3-12 Quality Review|bestpractice=UFR 3-12 Best Practice Advice|relatedACs=UFR 3-12 Related ACs}} | ||
Latest revision as of 13:15, 12 February 2017
Stagnation point flow
Underlying Flow Regime 3-12 © copyright ERCOFTAC 2004
Evaluation
Comparison of CFD calculations with Experiments
The following figures are taken from Medic (2001) and Medic and Durbin (2002), where the description is mainly taken from. Four different models (original k-ε, k-ε with T bound, Kato-Launders k-ε v2-f) were used and their respective predictions were compared with measurements.
Figure 1 shows the distribution of the isentropic Mach number Mis along the curvilinear co-ordinate s, normalised by the chord length and the origin placed at the stagnation point. The Mis distribution is not strongly affected by the choice of the turbulence model. The slightly lower values of the original k-ε model can be explained by attributing the excessive k (or νt) levels predicted by this model.
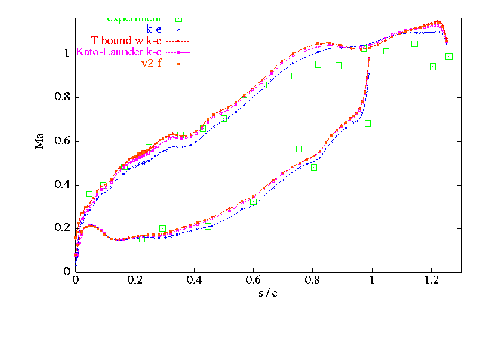
Fig. 1: Isentropic Mach number distribution along pressure and suction side for different turbulence models
The measured and predicted heat transfer coefficient ht, which is defined as ht = qw/(T0∞ − Tw), along the respective suction and pressure sides of the blade is shown in Figure 2. Significant differences among the various models can be observed here. The original k-ε model strongly over-predicts the heat transfer coefficient, especially on the pressure side towards the trailing edge. The same is reported for the original k-ω model by Medic and Durbin (2002). The levels of the predicted heat transfer by the Kato-Launder formulation or the bound on the turbulent time scale model (T bound) are much closer to the experiments. However, at the leading edge on the suction side ht is from both models over 30% too high. The predicted slope towards the trailing edge is steeper than from the measurements. On the other hand, the predictions of ht are better on the pressure side. This indicates the sensitivity of these two models (Kato-Launder and T bound) against an adverse pressure gradient. Of all four models considered in Medic (2001), the v2-f model yields the best results. This model is the only model which is able to capture the trough on the suction side of the experiments. Medic and Durbin (2002) pointed out, that this characteristic is due to the fact that the v2-f model is able to predict a reasonable transition location. However, on the pressure side this model under-predicts the recovery of the heat transfer coefficient towards the trailing edge. This may be caused by the tendency of the model towards relaminarisation of the flow (Medic and Durbin, 2002).
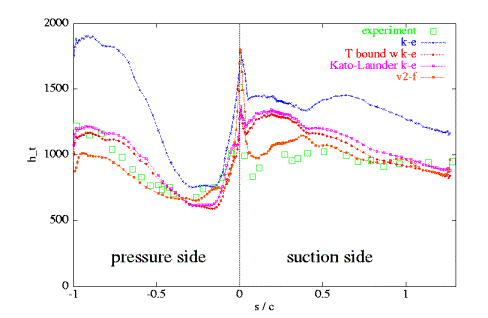
Fig. 2: Heat transfer coefficient ht distribution along pressure and suction side for different turbulence models
The heat transfer coefficient is related to the eddy viscosity, where the latter quantity is a function of the turbulent kinetic energy k. Therefore, the differences of the prediction of ht obtained from the different models can be directly linked to k. Figures 3 — 6 show the turbulent kinetic energy distribution predicted by the four considered models. Unfortunately, only computed values of this quantity are presented in Medic and Durbin (2002).
An outstanding feature of these results is that in the centre of the passage the turbulent kinetic energy levels predicted by the original k-ε model (or k-ω model) are about 30 times higher than from the v2-f model. Furthermore, the latter model shows a decrease of turbulent intensity in the centre passage in contrast to the former model.

Fig. 3: Iso-lines of turbulent kinetic energy for standard k-ε model.
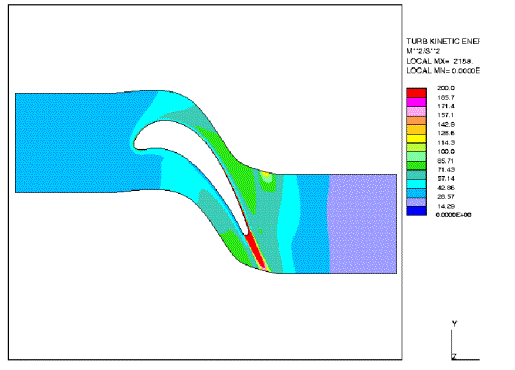
Fig. 4: Iso-lines of turbulent kinetic energy for v2-f model.
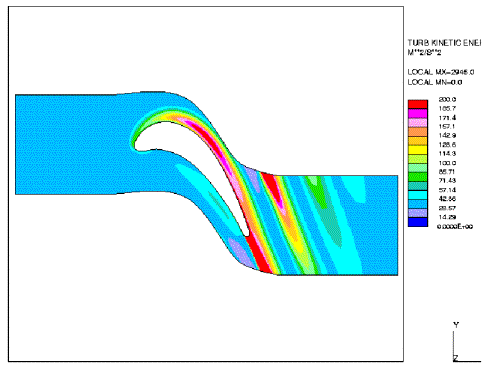
Fig. 5: Iso-lines of turbulent kinetic energy for k-ε model with modification according to Kato-Launder
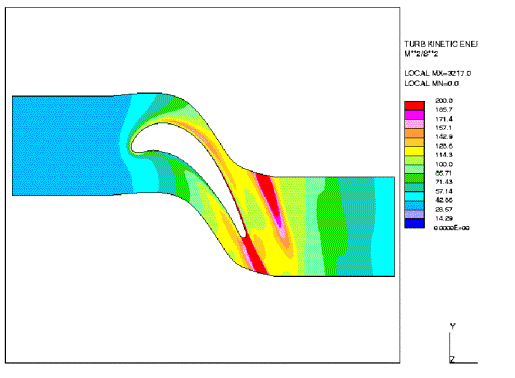
Fig. 6: Iso-lines of turbulent kinetic energy for k-ε model with bound on time scale
Conclusions
In simple cases one-equation models seem to be an option for the turbulence modelling, since these models do not experience a stagnation point anomaly. However, the problem of lack of information of the prescribed length scale restricts the use of one-equation models to a very limited range of cases.
The results from Medic and Durban (2002) suggest that an improvement of the performance of the standard k-ε or k-ω models is possible by using the v2-f model. Other options would be the implementation of a bound on the time scale or modifying the production term in the described manner, i.e. the Kato-Launder modification.
As mentioned above, higher order turbulence models may perform better than eddy-viscosity based models but are often not a practical option for many industrial applications. The recommendation is therefore to use — at least for applications with limited computer resources — models derived from the k-ε or k-ω formulation. Often for industrial purposes not the fine structure of turbulence is of interest, therefore the chosen model should be able to capture the main physical features of the flow field.
© copyright ERCOFTAC 2004
Contributors: Beat Ribi - MAN Turbomaschinen AG Schweiz