Description AC7-03: Difference between revisions
| (444 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
}} | }} | ||
__TOC__ | __TOC__ | ||
= | =Flow in a Ventricular Assist Device - Pump Performance & Blood Damage Prediction= | ||
'''Application Challenge AC7-03''' © copyright ERCOFTAC | '''Application Challenge AC7-03''' © copyright ERCOFTAC 2022 | ||
=Description= | =Description= | ||
==Introduction== | ==Introduction== | ||
Ventricular Assist Devices (VADs) are implanted in patients with severe heart failure. Today, nearly all VADs are designed as | Ventricular Assist Devices (VADs) are implanted in patients with severe heart failure. Today, nearly all VADs are designed as turbomachines, since they have a higher power density than pulsatile pumps. Therefore they can be implanted within the human body. Compared to Total Artificial Hearts (TAHs), the VADs do not replace the heart, but assist a weak heart by creating the pressure needed for supplying sufficient blood flow in the circulatory system. A few examples of VADs and TAHs currently implanted in patients can be seen in Figure 1.1. | ||
By using Computational Fluid Dynamics (CFD), VADs must be designed and optimised in such a way that they produce a physiological pressure increase sufficient to supply the body with enough blood flow. Furthermore, they must be designed so that the blood passing the VAD is not damaged due to non-physiological flow conditions (e.g., high shear stresses, stagnation areas and high turbulent kinetic energies (TKE)) in the device. | |||
The flow simulation in a VAD is challenging, since the inflow is laminar and all turbulence is produced within the pump and decays shortly after the pump outlet. In addition, complex interactions of secondary flows occur in the turbomachine, which must be taken into account in the flow simulation, since they influence the acting stresses in the flow of the VAD [2]. | |||
In this respect, the aim of this study is to investigate the suitability of the URANS method for the flow computation in an axial VAD. Here, both, fluid mechanical parameters, such as the pump characteristics, as well as hemodynamic parameters, such as the hemolysis index MIH, are investigated. The stress fields of the URANS will be compared with a highly turbulence-resolving large-eddy simulation, which represents the reference case for comparison. Furthermore, the influence of the grid resolution in the URANS computations will also be investigated based on an extended grid study. | |||
[[Image:VADs.jpg|600px|thumb|Fig.1.1 Total Artificial Hearts (TAHs) and Ventricular Assist Devices (VADs), which are currently in clinical use. One TAH, one pulsatile VAD and three turbo pumps are shown.]] | |||
==Relevance to Industrial Sector== | ==Relevance to Industrial Sector== | ||
When the VAD designer is able to find a good VAD design by CFD, | The flow computation in a Ventricular Assist Device (VAD) is an important procedure for the VAD design and optimization in the pre-clinical evaluation. The aims of these CFD studies are, on one hand, to guarantee that the VAD offers the physiologically relevant pressure increase at the chosen operating points to sufficiently support the VAD patient. On the other hand, hemodynamical parameters must be evaluated in these studies. Here, it is important that the CFD indicates relevant regions for potential blood damage or thrombi formation so that these regions can be minimized in the optimization procedure. Additionally, CFD is important for comparing different designs in order to find the pump with the highest hemocompatibility (lowest blood damage). | ||
When the VAD designer is able to find a good VAD design by CFD, the amount of in-vitro (experimental test of pump performance or hemolysis (red blood cell damage)) and in-vivo testing (animal trials) might be reduced. | |||
==Flow Domain Geometry== | |||
The geometry of the VAD is available at the link: https://unibox.uni-rostock.de/getlink/fi8AE4mYS4kxu8ZY51oxDh/ | |||
The investigated axial VAD is illustrated within the computational domain in Fig. 1.2. It consist of a spinning rotor with two blade channels; a stationary, inlet guide vane with five blades; and a stationary, three-bladed outlet guide vane. While the transfer of angular momentum via the rotor leads to an increase in pressure and velocity (swirl formation), the swirl is converted back into static pressure by the diffuser effect in the outlet guide vane. The inlet guide vane is intended for flow manipulation of the rotor inflow. In the present VAD, a counter-rotation is generated, which theoretically leads to a flatter pressure head curve. | |||
This axial VAD has been designed at the Institute of Turbomachinery at the University of Rostock. The design was inspired by axial VADs, which are currently in clinical use. The design principles are briefly explained: After chosing the inner (<math> D_1 = 11~mm </math>) and outer (<math> D_2 = 16~mm </math>) diameter, meridian lines were placed between hub and casing to set the blades angles for a chosen nominal operation point <math> (Q=4.5~l/min,~n=7900~r/min) </math>. Afterward, the wrap angle of the blades was adjusted to obtain an even blade progression. After that, the blade thickness and gap height (distance between the casing and the rotor's blade tip; <math> 120~\mu m </math>) were included. The outlet guide vanes were set up so that the swirl is reduced as much as possible. Finally, the coupled rotor and stator were adjusted using URANS simulations, until the pump achieved a pressure head of <math> H=(70-80)~mmHg </math> and a hydraulic effiency of <math> \eta_i \approx 33 \% </math> at the nominal operating point. | |||
This VAD was designed for reseach purposes only. The aim of the design was not to build a "perfect" implantable VAD with an optimal flow behaviour, but rather a pump, in which the same flow pattern can occur as in real implanted VADs. In these pumps, the inflow angle cannot be optimal during the entire operation time due to varying input from the remaining heart activity. Thus, non-optimal inflow angles and flow paths were delibaretely accepted at the nominal operation point. | |||
[[Image:FlowGeometry.gif|500px|center|thumb|Fig.1.2 VAD geometry in a part of the computational domain (inflow and outflow cannulas are much longer in the computational model). The VAD's casing (sketched as black lines) is the radial boundary of the computational domain).]] | |||
==Design or Assessment Parameters== | ==Design or Assessment Parameters== | ||
The main assessment parameters for this | The main assessment parameters for this study are: | ||
* Pressure increase via the VAD (pressure head) <math> H </math> | * Pressure increase via the VAD ('''pressure head''') <math> H </math> | ||
* Hydraulic efficiency of the pump <math> \eta_i </math> | * Hydraulic efficiency of the pump <math> \eta_i </math> | ||
* equivalent | * equivalent stress <math> \tau_s </math> or effective stress <math> \tau_{eff} </math> | ||
* Modified index of hemolysis <math> MIH </math> | * Modified index of hemolysis <math> MIH </math> | ||
* | * Volumes, in which certain stress thresholds <math> I_{\tau_s \geq threshold} </math> are exceeded (volumentric analysis) | ||
The rationale behind these parameters and details of how to calculate each of them are described below. | |||
* '''Pressure head''' | * '''Pressure head''' | ||
| Line 41: | Line 56: | ||
The pressure increase via a VAD is typically defined in millimeters of mercury <math> [mmHg] </math>: | The pressure increase via a VAD is typically defined in millimeters of mercury <math> [mmHg] </math>: | ||
<center><math> H = \sum_{outlet} \langle p_{tot} \rangle \qquad\qquad\qquad\qquad(1) </math><center> | <center><math> H = \frac{\sum_{outlet} \langle p_{tot} \rangle \cdot \dot{m}_{cell}}{\sum_{outlet} \dot{m}_{cell}}-\frac{\sum_{inlet} \langle p_{tot} \rangle \cdot \dot{m}_{cell}}{\sum_{inlet} \dot{m}_{cell}} \qquad\qquad\qquad\qquad(1) </math></center> | ||
with <math> \langle p_{tot} \rangle </math> as the time-averaged total pressure and <math> \dot{m}_{cell} </math> as the mass flow in each cell. These variables are massflow-averaged by taking the sum over the cells at the outlet and inlet. | |||
* '''Inner efficiency''' | |||
The inner efficiency balances the fluid power that the VAD realizes in the form of a pressure increase <math> H </math> and fluid transport <math> Q </math>, compared to the power required to make the VAD's impeller rotate with a certain torque <math> M </math> and rotational speed <math> n </math>. | |||
<center><math> \eta_i = \frac{H \cdot Q}{M \cdot 2 \pi n} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2) </math></center> | |||
The blade torque <math> M </math> is determined at the rotating surfaces of the impeller by accounting for the surface pressures <math> p_{sf} </math> and surface shear stresses <math> \tau_{sf} </math> (e.g. the impeller rotates around the z-axis, S denotes the impeller surface): | |||
<center><math> M_z = \langle \big[ \int_S{r_s \times (n_s p_{sf} dS)} + \int_S{r_s \times (t_s \tau_{sf} dS)} \big] \cdot e_z \rangle \qquad\qquad\qquad(3) </math></center> | |||
with: | |||
* <math> t_s </math> - unit parallel vector | |||
* <math> n_s </math> - unit vector parallel to <math> dS </math> | |||
* <math> e_z </math> - unit vector parallel to the z-axis | |||
Two types of inner efficiencies will be evaluated in section [[Evaluation AC7-03|Evaluation]]. Firstly, the inner efficiency of the whole pump (index: <math> p </math>) and secondly, the inner efficiency of the impeller alone (index: <math> i </math>). Both types were determined respectively with the pressure build-up at the corresponding domain boundaries. | |||
* '''Equivalent and effective shear stress''' | |||
The equivalent shear stress <math> \tau_s </math> is the parameter, by which blood damage is predicted in blood simulations in complex flow geometries. The basis for this parameter derives from the shear stress tensor <math> \tau_{ij} </math>, which contains the instantaneous spatial gradients of the velocity <math> u_i </math>: | |||
<center><math> \tau_{ij}= \mu ( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(4) </math></center> | |||
For blood damage prediction in complex, three-dimensional flows, the stress tensor <math> \tau_{ij} </math> is reduced to a scalar representation - the equivalent shear stress <math> \tau_s </math>. Most numerical VAD simulations use a formulation based on the second invariant of the rate-of-strain tensor <math> S_{ij} </math>: | |||
<center><math> \tau_{s}= \mu \sqrt{2 S_{ij} S_{ij}} </math>, with <math>S_{ij}=\frac{1}{2}( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i})\qquad\qquad\qquad\qquad\qquad(5) </math></center> | |||
In URANS and LES methods, the instantaneous velocities are decomposed into a resolved component and an unresolved component. Accordingly, the instantaneous strain rate <math> S_{ij} </math> is decomposed into a resolved variable <math> \overline{S}_{ij} </math> and an unresolved component <math> S_{ij}^' </math>: | |||
<center><math> S_{ij}= \overline{S}_{ij} + S_{ij}^', \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(6) </math></center> | |||
In URANS with unsteady mean flow, <math> \overline{S}_{ij} </math> is an ensemble average (but can be considered as time-average, when the averaging time is long compared to the time scales of turbulent motions). In LES, <math> \overline{S}_{ij} </math> is the instantaneous, resolved value (with the sub-grid scale fluctuations filtered out) and <math> S_{ij}^' </math> are the subgrid-scale (SGS) fluctuations. This decomposition leads to the following expression for the equivalent stresses: | |||
<center><math> \tau_{s}= \mu \sqrt{2 ( \overline{S}_{ij} \overline{S}_{ij} + 2 \overline{S}_{ij} S_{ij}' + S_{ij}' S_{ij}')} \qquad\qquad\qquad\qquad\qquad\qquad(7) </math></center> | |||
Taking the square of <math> \tau_s </math> and applying the averaging (URANS) or filtering (LES) leads to an instantaneous, effective stress <math> \tau_{eff} </math>, which, when introducing the kinematic viscosity <math> \nu = \mu / \rho </math>, can be related to the dissipation of kinetic energy: | |||
<center><math> \tau_{eff} = \sqrt{\overline{\tau_s^2}}= \mu \sqrt{2 \overline{S}_{ij} \overline{S}_{ij} + 2 \overline{S_{ij}' S_{ij}'}} = \mu \sqrt{\frac{1}{\nu} \underbrace{ 2 \nu \overline{S}_{ij} \overline{S}_{ij} }_\text{direct dissipation} + \frac{1}{\nu} \underbrace{ 2 \nu \overline{S_{ij}' S_{ij}'}}_\text{turbulent dissipation}} (8) </math></center> | |||
Here, the first part is the direct viscous dissipation, which can be calculated from the resolved instantaneous strain rates <math> \overline{S}_{ij} </math>. On the other hand, the second part is the turbulent dissipation <math> \varepsilon_{turb} </math> as defined in equation (8) - in URANS it is the entire turbulent dissipation and in LES the dissipation by the sugrid-scale motion. This second part needs to be obtained from a model and is generally the dominant contributor to the dissipation in a fully turbulent flow. | |||
For URANS, <math> \varepsilon_{turb} </math> is given by the turbulence model (e.g., <math> \varepsilon = k\cdot \omega </math> in the applied <math> k </math> - <math> \omega </math>-SST model). For our LES it is given by[6]: | |||
<center><math> \varepsilon_{turb} = \nu_{t,SGS}||{\overline{S}_{ij}}^2||, \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(9) </math></center> | |||
where <math> \nu_{t,SGS} </math> is the subgrid-scale eddy viscosity determined by the Smagorinsky SGS model. | |||
As a result, the effective stress <math> \tau_{eff} </math>, which is used for URANS and LES, is obtained from: | |||
<center><math> \tau_{eff} = \mu \sqrt{2 \overline{S}_{ij} \overline{S}_{ij} + (1/\nu) \varepsilon_{turb}} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(10) </math></center> | |||
Please note that <math> \tau_{eff} </math> in Eq. (10) is still an instantaneous value (as shown in Fig. 1.3). A time-averaged, effective stress <math> \langle \tau_{eff} \rangle </math> is defined as the last step and this variable is used for the blood damage evaluation in section [[Evaluation AC7-03|Evaluation]] and shown there in Fig. 5.2. | |||
* '''Modified hemolysis index''' | |||
The modified index of hemoylsis <math> MIH </math> is a widely used parameter to numerically assess hemolysis in VADs [3-6]. Hemolysis denotes the rupture of red blood cells. The ruptured cells release their hemoglobin into the blood plasma, which can lead to serious complications, like anemia or organ damage. A large number of numerical hemolysis prediction models are based on power laws. These models establish a direct relationship between hemolysis <math> MIH </math>, an equivalent or effective stress <math> \tau_{eff} </math> and the exposure time <math> t </math>. Experimentally determined constants <math> (\alpha;\beta;C) </math> are used | |||
to combine the variables to an MIH-value: | |||
<center><math> MIH= H_l \cdot 10^6= C \cdot \langle \tau_{eff} \rangle ^{\alpha} \cdot t^{\beta} \cdot 10^6. \qquad\qquad\qquad\qquad\qquad\qquad\qquad(11) </math></center> | |||
The hemolysis value <math> H_l(\tau_{eff}, t) </math> and the exposure time <math> t </math> are needed to compute the MIH-value in the equation above. | |||
For numerical design and optimization studies, the MIH-value is tranformed into a formulation, which can be directly calculated from the computed, time-averaged flow field. This results in Eq. (11), which is also used in the present ERCOFTAC KB Wiki entry. The exact derivations of Eq. (10) to Eq. (11) are not given here, but can be found in Ref. [7]. | |||
<center><math> {MIH}= \frac{1}{Q} \int_V{(C^{1/\beta} \langle \tau_{eff} \rangle ^{\alpha / \beta}})dV)^{\beta}\cdot 10^6 \qquad\qquad\qquad\qquad\qquad\qquad\qquad(12) </math></center> | |||
* '''Volumetric analysis of stress thresholds''' | |||
In this blood damage prediction model, which is widely used for design purposes, volumes <math> I_{\tau_{eff} \geq threshold} </math> are calculated in the computational domain, which exceed certain stress thresholds. Three blood damage types can be analysed. For hemolysis, a stress threshold of <math> \langle \tau_{eff} \rangle \geq 150~Pa </math> is defined. Additionally, this model addresses the degradation of von-Willebrandt proteins. Internal bleeding could happen, when this type of protein damage occurs. A stress threshold of <math> \langle \tau_{eff} \rangle \geq 9~Pa </math> is given for the protein damage. Also, a stress threshold for the activation of thrombocytes is defined with <math> \langle \tau_{eff} \rangle \geq 50~Pa </math>. The activation of thrombocytes could lead to a formation of a white thrombus, which can lead to a thromboembolic event or a pump thrombosis. | |||
==Flow Physics and Fluid Dynamics Data== | ==Flow Physics and Fluid Dynamics Data== | ||
< | The VAD was analysed at the nominal load (<math> Q=4.5~l/min </math> ) and partial load (<math> Q=2.5~l/min </math> ) operating point at a rotational speed of <math> n=7900~1/min </math>. These conditions result in a Reynolds number of <math> Re_p=u_2\cdot D_2 / \nu =3\cdot 10^4 </math> (at both operation points under investigation). Here, <math> u_2 </math> denotes the circumferential velocity of the blades near the casing (with a diameter of <math> D_2 </math>). This pump Reynolds number <math> Re_p </math> is comparable to the range of Reynolds numbers found in other blood pumps [10]. | ||
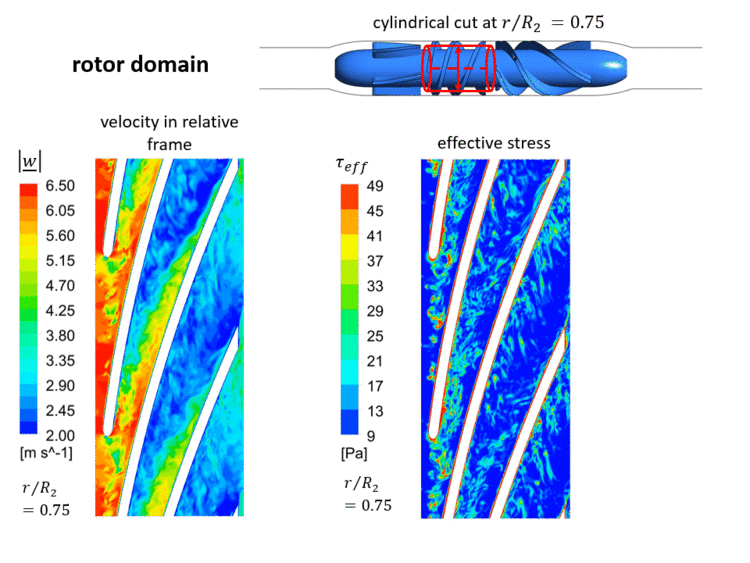
At the inlet of the VAD, a laminar inflow can be assumed, since the pipe Reynolds number based on the hydraulic diameter <math> D_h </math> of the inlet cannula is small <math> Re_{cannula}=c_{cannula} \cdot D_{cannula} / \nu \approx 2300 </math>. Hence, all (coherent and turbulent) fluctuations and the associated stresses in the VAD's flow will be produced within the pump. The instantaneous velocities and instantaneous effective stresses in the rotor domain are shown in an animated Figure 1.3 in a cylindrical cut at 0.75 of the casing's radius <math> R_2 </math>. | |||
As displayed in that figure, an unsteady flow develops already at the inlet of the rotor channel. This is triggered by the fluctuating gap vortex in this inlet region, which comes as a result of the superposition of the main flow and a secondary flow from the rotor gap (region between rotor tip and casing). Increased effective stresses are observable in this gap vortex, which have a significant impact on the numerical blood damage prediction (analyzed in section [[Evaluation AC7-03|Evaluation]]). Additionally, further secondary flows - which are typical for turbomachinery flows - such as the passage or horseshoe vortex, interact with each other in the VAD's blade channels, resulting in increased instanteous effective stresses. A detailed analysis of sources of effective stresses in the VAD can be found in Refs. [2] and [27]. | |||
[[Image:Test_FlowPhysics.gif|750px|center|thumb|Fig.1.3 Instantaneous flow in the rotor domain computed by LES '''(please click twice on this figure for an animated view)'''. Visualised on a cylindrical cut at 0.75 of the casing's radius. Left: Velocity in the relative frame of reference. Right: Effective stresses (Eq. (10)). Please note that <math> r/R_2=0 </math> is located at the rotor's hub.]] | |||
---- | ---- | ||
{{ACContribs | {{ACContribs | ||
| Line 56: | Line 150: | ||
}} | }} | ||
© copyright ERCOFTAC | © copyright ERCOFTAC 2022 | ||
Latest revision as of 05:47, 17 July 2023
Flow in a Ventricular Assist Device - Pump Performance & Blood Damage Prediction
Application Challenge AC7-03 © copyright ERCOFTAC 2022
Description
Introduction
Ventricular Assist Devices (VADs) are implanted in patients with severe heart failure. Today, nearly all VADs are designed as turbomachines, since they have a higher power density than pulsatile pumps. Therefore they can be implanted within the human body. Compared to Total Artificial Hearts (TAHs), the VADs do not replace the heart, but assist a weak heart by creating the pressure needed for supplying sufficient blood flow in the circulatory system. A few examples of VADs and TAHs currently implanted in patients can be seen in Figure 1.1.
By using Computational Fluid Dynamics (CFD), VADs must be designed and optimised in such a way that they produce a physiological pressure increase sufficient to supply the body with enough blood flow. Furthermore, they must be designed so that the blood passing the VAD is not damaged due to non-physiological flow conditions (e.g., high shear stresses, stagnation areas and high turbulent kinetic energies (TKE)) in the device.
The flow simulation in a VAD is challenging, since the inflow is laminar and all turbulence is produced within the pump and decays shortly after the pump outlet. In addition, complex interactions of secondary flows occur in the turbomachine, which must be taken into account in the flow simulation, since they influence the acting stresses in the flow of the VAD [2].
In this respect, the aim of this study is to investigate the suitability of the URANS method for the flow computation in an axial VAD. Here, both, fluid mechanical parameters, such as the pump characteristics, as well as hemodynamic parameters, such as the hemolysis index MIH, are investigated. The stress fields of the URANS will be compared with a highly turbulence-resolving large-eddy simulation, which represents the reference case for comparison. Furthermore, the influence of the grid resolution in the URANS computations will also be investigated based on an extended grid study.
Relevance to Industrial Sector
The flow computation in a Ventricular Assist Device (VAD) is an important procedure for the VAD design and optimization in the pre-clinical evaluation. The aims of these CFD studies are, on one hand, to guarantee that the VAD offers the physiologically relevant pressure increase at the chosen operating points to sufficiently support the VAD patient. On the other hand, hemodynamical parameters must be evaluated in these studies. Here, it is important that the CFD indicates relevant regions for potential blood damage or thrombi formation so that these regions can be minimized in the optimization procedure. Additionally, CFD is important for comparing different designs in order to find the pump with the highest hemocompatibility (lowest blood damage).
When the VAD designer is able to find a good VAD design by CFD, the amount of in-vitro (experimental test of pump performance or hemolysis (red blood cell damage)) and in-vivo testing (animal trials) might be reduced.
Flow Domain Geometry
The geometry of the VAD is available at the link: https://unibox.uni-rostock.de/getlink/fi8AE4mYS4kxu8ZY51oxDh/
The investigated axial VAD is illustrated within the computational domain in Fig. 1.2. It consist of a spinning rotor with two blade channels; a stationary, inlet guide vane with five blades; and a stationary, three-bladed outlet guide vane. While the transfer of angular momentum via the rotor leads to an increase in pressure and velocity (swirl formation), the swirl is converted back into static pressure by the diffuser effect in the outlet guide vane. The inlet guide vane is intended for flow manipulation of the rotor inflow. In the present VAD, a counter-rotation is generated, which theoretically leads to a flatter pressure head curve.
This axial VAD has been designed at the Institute of Turbomachinery at the University of Rostock. The design was inspired by axial VADs, which are currently in clinical use. The design principles are briefly explained: After chosing the inner () and outer () diameter, meridian lines were placed between hub and casing to set the blades angles for a chosen nominal operation point . Afterward, the wrap angle of the blades was adjusted to obtain an even blade progression. After that, the blade thickness and gap height (distance between the casing and the rotor's blade tip; ) were included. The outlet guide vanes were set up so that the swirl is reduced as much as possible. Finally, the coupled rotor and stator were adjusted using URANS simulations, until the pump achieved a pressure head of and a hydraulic effiency of at the nominal operating point.
This VAD was designed for reseach purposes only. The aim of the design was not to build a "perfect" implantable VAD with an optimal flow behaviour, but rather a pump, in which the same flow pattern can occur as in real implanted VADs. In these pumps, the inflow angle cannot be optimal during the entire operation time due to varying input from the remaining heart activity. Thus, non-optimal inflow angles and flow paths were delibaretely accepted at the nominal operation point.
Design or Assessment Parameters
The main assessment parameters for this study are:
- Pressure increase via the VAD (pressure head)
- Hydraulic efficiency of the pump
- equivalent stress or effective stress
- Modified index of hemolysis
- Volumes, in which certain stress thresholds are exceeded (volumentric analysis)
The rationale behind these parameters and details of how to calculate each of them are described below.
- Pressure head
The pressure increase via a VAD is typically defined in millimeters of mercury :
with as the time-averaged total pressure and as the mass flow in each cell. These variables are massflow-averaged by taking the sum over the cells at the outlet and inlet.
- Inner efficiency
The inner efficiency balances the fluid power that the VAD realizes in the form of a pressure increase and fluid transport , compared to the power required to make the VAD's impeller rotate with a certain torque and rotational speed .
The blade torque is determined at the rotating surfaces of the impeller by accounting for the surface pressures and surface shear stresses (e.g. the impeller rotates around the z-axis, S denotes the impeller surface):
with:
- - unit parallel vector
- - unit vector parallel to
- - unit vector parallel to the z-axis
Two types of inner efficiencies will be evaluated in section Evaluation. Firstly, the inner efficiency of the whole pump (index: ) and secondly, the inner efficiency of the impeller alone (index: ). Both types were determined respectively with the pressure build-up at the corresponding domain boundaries.
- Equivalent and effective shear stress
The equivalent shear stress is the parameter, by which blood damage is predicted in blood simulations in complex flow geometries. The basis for this parameter derives from the shear stress tensor , which contains the instantaneous spatial gradients of the velocity :
For blood damage prediction in complex, three-dimensional flows, the stress tensor is reduced to a scalar representation - the equivalent shear stress . Most numerical VAD simulations use a formulation based on the second invariant of the rate-of-strain tensor :
In URANS and LES methods, the instantaneous velocities are decomposed into a resolved component and an unresolved component. Accordingly, the instantaneous strain rate is decomposed into a resolved variable and an unresolved component :
In URANS with unsteady mean flow, is an ensemble average (but can be considered as time-average, when the averaging time is long compared to the time scales of turbulent motions). In LES, is the instantaneous, resolved value (with the sub-grid scale fluctuations filtered out) and are the subgrid-scale (SGS) fluctuations. This decomposition leads to the following expression for the equivalent stresses:
Taking the square of and applying the averaging (URANS) or filtering (LES) leads to an instantaneous, effective stress , which, when introducing the kinematic viscosity , can be related to the dissipation of kinetic energy:
Here, the first part is the direct viscous dissipation, which can be calculated from the resolved instantaneous strain rates . On the other hand, the second part is the turbulent dissipation as defined in equation (8) - in URANS it is the entire turbulent dissipation and in LES the dissipation by the sugrid-scale motion. This second part needs to be obtained from a model and is generally the dominant contributor to the dissipation in a fully turbulent flow.
For URANS, is given by the turbulence model (e.g., in the applied - -SST model). For our LES it is given by[6]:
where is the subgrid-scale eddy viscosity determined by the Smagorinsky SGS model.
As a result, the effective stress , which is used for URANS and LES, is obtained from:
Please note that in Eq. (10) is still an instantaneous value (as shown in Fig. 1.3). A time-averaged, effective stress is defined as the last step and this variable is used for the blood damage evaluation in section Evaluation and shown there in Fig. 5.2.
- Modified hemolysis index
The modified index of hemoylsis is a widely used parameter to numerically assess hemolysis in VADs [3-6]. Hemolysis denotes the rupture of red blood cells. The ruptured cells release their hemoglobin into the blood plasma, which can lead to serious complications, like anemia or organ damage. A large number of numerical hemolysis prediction models are based on power laws. These models establish a direct relationship between hemolysis , an equivalent or effective stress and the exposure time . Experimentally determined constants are used to combine the variables to an MIH-value:
The hemolysis value and the exposure time are needed to compute the MIH-value in the equation above. For numerical design and optimization studies, the MIH-value is tranformed into a formulation, which can be directly calculated from the computed, time-averaged flow field. This results in Eq. (11), which is also used in the present ERCOFTAC KB Wiki entry. The exact derivations of Eq. (10) to Eq. (11) are not given here, but can be found in Ref. [7].
- Volumetric analysis of stress thresholds
In this blood damage prediction model, which is widely used for design purposes, volumes are calculated in the computational domain, which exceed certain stress thresholds. Three blood damage types can be analysed. For hemolysis, a stress threshold of is defined. Additionally, this model addresses the degradation of von-Willebrandt proteins. Internal bleeding could happen, when this type of protein damage occurs. A stress threshold of is given for the protein damage. Also, a stress threshold for the activation of thrombocytes is defined with . The activation of thrombocytes could lead to a formation of a white thrombus, which can lead to a thromboembolic event or a pump thrombosis.
Flow Physics and Fluid Dynamics Data
The VAD was analysed at the nominal load ( ) and partial load ( ) operating point at a rotational speed of . These conditions result in a Reynolds number of (at both operation points under investigation). Here, denotes the circumferential velocity of the blades near the casing (with a diameter of ). This pump Reynolds number is comparable to the range of Reynolds numbers found in other blood pumps [10].
At the inlet of the VAD, a laminar inflow can be assumed, since the pipe Reynolds number based on the hydraulic diameter of the inlet cannula is small . Hence, all (coherent and turbulent) fluctuations and the associated stresses in the VAD's flow will be produced within the pump. The instantaneous velocities and instantaneous effective stresses in the rotor domain are shown in an animated Figure 1.3 in a cylindrical cut at 0.75 of the casing's radius . As displayed in that figure, an unsteady flow develops already at the inlet of the rotor channel. This is triggered by the fluctuating gap vortex in this inlet region, which comes as a result of the superposition of the main flow and a secondary flow from the rotor gap (region between rotor tip and casing). Increased effective stresses are observable in this gap vortex, which have a significant impact on the numerical blood damage prediction (analyzed in section Evaluation). Additionally, further secondary flows - which are typical for turbomachinery flows - such as the passage or horseshoe vortex, interact with each other in the VAD's blade channels, resulting in increased instanteous effective stresses. A detailed analysis of sources of effective stresses in the VAD can be found in Refs. [2] and [27].
Contributed by: B. Torner — University of Rostock, Germany
© copyright ERCOFTAC 2022














![{\displaystyle [mmHg]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dfb5d7ba57c453181e40d1d887d4cbbd472d8856)









![{\displaystyle M_{z}=\langle {\big [}\int _{S}{r_{s}\times (n_{s}p_{sf}dS)}+\int _{S}{r_{s}\times (t_{s}\tau _{sf}dS)}{\big ]}\cdot e_{z}\rangle \qquad \qquad \qquad (3)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/66367a014d3ba4663a08ab279d58ad6a0419216b)













































